揭秘梯形体积计算的神秘公式！

在几何学的广阔领域中，梯形作为一种特殊的四边形，因其一对平行边不等长的特性而独具魅力。当我们谈及梯形的体积时，首先需要澄清一个常见的误区：在二维平面上，梯形作为一个平面图形，其本身并不具备体积属性，体积是三维空间中的概念。然而，当梯形作为一个底面，与其他几何形状（如矩形、三角形或另一个梯形）结合形成三维立体时，如棱台或梯形体，我们就可以探讨其体积了。本文将从定义、推导、应用及生活实例等多个维度，深入探讨与梯形相关的体积公式。

一、梯形的基本定义与性质

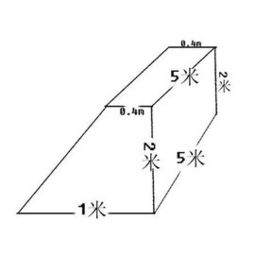
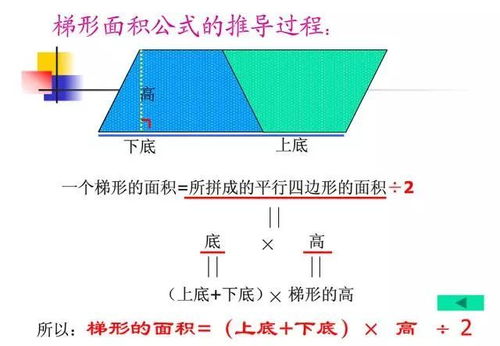
梯形，作为一种四边形，具有一对平行的直线段作为上底和下底，而另外两边则为非平行的腰。设梯形的上底长度为a，下底长度为b，高为h。梯形的面积公式为：面积 = (a + b) × h / 2，这是通过分割梯形为两个三角形和一个矩形（或平行四边形），再求和得到的。

二、梯形体与棱台的体积公式推导

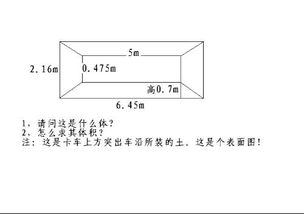
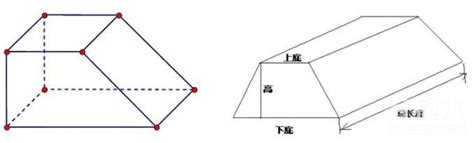
当我们把梯形扩展到三维空间，形成梯形体（或称为截头棱柱）时，其体积计算就变得复杂起来。梯形体是指由两个平行且相似的梯形面以及连接这两个梯形对应顶点的四个侧面围成的立体。为了推导梯形体的体积公式，我们可以采用积分法或几何法。

积分法推导

想象一个梯形底面逐渐上升（或下降），形成另一个相似的梯形底面，这一过程中形成的立体即为梯形体。通过微积分中的“壳层法”或“切片法”，我们可以将梯形体看作是由无数个微小的梯形（或矩形，当高度变化非常微小时）沿垂直方向堆叠而成。每一微小梯形的面积可以近似表示为A(y) = (a + ky) × dy / 2，其中k是上下底长度变化的比例系数，dy是微小高度变化量。对整个高度H进行积分，即可得到梯形体的体积：

V = ∫[0,H] A(y) dy = ∫[0,H] (a + ky) × dy / 2 = [ay + ky²/2]₀ᴴ / 2 = (aH + kH²/2)H/2 = (a + kb/2)H²/2 - (a + ka/2)×0²/2 = (a + b)H² / 4（因为b = a + kH），其中H为梯形体的总高，b为下底长，a为上底长。

简化后得到梯形体体积公式：V = (a + b)H² / 4。

几何法推导

另一种更直观的方法是使用几何相似性。设想将梯形体补全为一个长方体，然后减去多余的部分（即顶部和底部的三角形棱锥）。长方体的体积为(a + b) × H × l（l为长方体的另一维度，对于梯形体而言，它可以是连接上下底对应点的任意线段，但在体积计算中不影响最终结果，因为最终会被约去）。而顶部和底部的三角形棱锥体积之和可以通过它们的底面积和高来计算，并做适当的减法调整。经过推导，同样可以得到梯形体的体积公式：V = (a + b)H² / 4。

对于棱台（特别是截头四棱台，即上下底面为矩形的棱台，若其侧面为梯形则也可视为特殊类型的梯形体），其体积公式可通过类似的方法推导，但考虑到其底面为矩形，计算过程中会涉及到矩形面积而非梯形面积。棱台的体积公式为：V = (S1 + S2 + √(S1S2))h / 3，其中S1和S2分别为上下底面积，h为高。

三、梯形体积公式的应用

梯形体积公式在工程设计、土木工程、建筑学等领域有着广泛的应用。例如，在设计水库大坝、桥梁的桥墩、建筑物的地下室等结构时，经常需要计算由梯形截面构成的柱体或棱台的体积，以确保结构的稳定性和材料的合理分配。此外，在农业灌溉系统中，梯形渠道的设计也需要用到梯形体积公式来计算水流量和渠道容量。

工程实例

1. 水库大坝：大坝的横截面往往设计成梯形，以优化稳定性和抗冲刷能力。通过测量上底、下底和高，可以精确计算大坝各段的体积，进而估算所需的建筑材料量。

2. 桥梁桥墩：桥墩作为支撑桥梁结构的关键部件，其形状和尺寸需经过精确计算。采用梯形截面的桥墩，可以利用梯形体积公式快速计算其体积，为施工提供重要参数。

3. 地下室设计：在建筑设计中，地下室往往采用梯形截面以增加空间利用率和稳定性。通过梯形体积公式，可以方便地计算出地下室各部分的体积，