揭秘梯形体积计算：轻松掌握公式秘籍

在几何学中，梯形是一种四边形，其特点是一对平行的对边，通常被称为上底和下底，而另外一对非平行的对边则称为腰。当我们尝试计算三维空间中的梯形体积时，实际上是在处理一个棱台，它可以被视作由两个相似的梯形作为底面，并通过平行于底面的面连接而成的几何体。因此，要计算所谓的“梯形体积”，我们实际上是在计算棱台的体积。下面，我们将从定义、基本公式、推导过程、实际应用以及与其他几何体比较的多个维度来详细探讨棱台体积的计算方法。

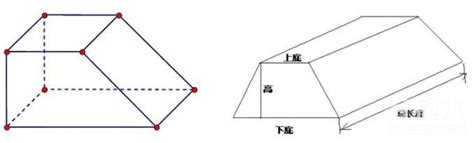
定义

棱台是一种多面体，其底面与顶面是相似的多边形，且侧面为梯形或平行四边形。根据底面的形状，棱台可以分为不同的类型，如三棱台、四棱台（即梯形棱台）等。当我们提及梯形的体积时，通常指的是四棱台的体积，因为四棱台的底面与顶面都是梯形。

基本公式

棱台的体积计算公式是：

\[V = \frac{1}{3}h(S_1 + S_2 + \sqrt{S_1S_2})\]

其中：

\(V\) 是棱台的体积。

\(h\) 是棱台的高，即底面与顶面之间的距离。

\(S_1\) 是棱台的上底面积。

\(S_2\) 是棱台的下底面积。

\(\sqrt{S_1S_2}\) 是上底面积与下底面积几何平均值的平方根。

推导过程

为了理解这个公式的来源，我们可以采用几何分割法或积分法来推导。

几何分割法

假设我们有一个棱台，可以通过构造一个与棱台等高、底面与棱台的上底相同的棱柱，以及一个与棱台的下底相同、高度为棱台高度差的棱锥，来进行几何分割。首先，用棱柱的体积减去棱锥的体积可以得到一个中间体的体积，这个中间体可以近似看作棱台的一部分（但实际上并不完全相同，因为棱台侧面是梯形而非矩形）。通过不断调整棱锥的高度，使得中间体越来越接近棱台，最终可以通过极限的思想证明，当分割足够细密时，这些中间体的体积之和就趋近于棱台的体积。

然而，这种方法虽然直观，但在实际计算中并不方便，因此更多时候我们采用积分法来推导公式。

积分法

考虑到棱台可以看作是一个沿着垂直于底面方向逐渐变化的梯形面积的累积，我们可以使用定积分来表示棱台的体积。设棱台的高为\(h\)，底面（梯形）的面积从\(S_1\)（上底）变化到\(S_2\)（下底），则棱台的体积可以表示为：

\[V = \int_{0}^{h} A(x) \, dx\]

其中\(A(x)\)是棱台在高度\(x\)处的横截面积。由于棱台的上下底面是相似的梯形，因此横截面积\(A(x)\)与\(x\)成线性关系。通过求解这个积分，我们可以得到棱台的体积公式：

\[V = \frac{1}{3}h(S_1 + S_2 + \sqrt{S_1S_2})\]

实际应用

棱台体积的计算在建筑、土木工程、水利等领域有着广泛的应用。例如，在计算水库的蓄水量时，如果水库的形状可以近似看作棱台，那么我们就可以使用棱台的体积公式来估算蓄水量。同样，在建筑设计中，如果某些结构部分可以看作棱台形状，那么计算其体积也是设计过程中的重要步骤。

水库蓄水量计算

假设一个水库的形状可以近似看作一个四棱台，已知其上底面积为\(S_1\)，下底面积为\(S_2\)，高度为\(h\)，则可以使用棱台的体积公式来计算水库的蓄水量。

建筑结构设计

在建筑设计中，如果某个结构部分如楼梯间、电梯井等可以看作棱台形状，那么计算其体积对于材料估算和成本控制至关重要。通过测量或设计参数确定上底面积、下底面积和高度后，即可使用棱台体积公式进行计算。

与其他几何体比较

棱台与其他几何体在体积计算上既有相似之处，也有其独特之处。

与棱柱的比较

棱柱是一种底面为多边形、侧面为矩形的多面体。棱柱的体积计算公式为底面积乘以高，即\(V = Sh\)。与棱台相比，棱柱的底面是固定的多边形，而棱台的底面是变化的梯形。此外，棱柱的侧面是矩形，而棱台的侧面是梯形。因此，在计算体积时，棱柱更为简单直接，