二进制与八进制相互转换方法
在计算机科学和数字系统的基础中,二进制和八进制扮演着至关重要的角色。二进制,作为计算机内部信息处理的基础,其简洁性和直接性无可替代;而八进制,作为二进制的一种紧凑表示形式,则在某些应用场景中展现出独特的优势。本文将深入探讨二进制与八进制之间的转换方法,从基本原理、步骤解析、实际应用以及数学逻辑等多个维度进行阐述,旨在帮助读者全面理解这两种进制间的转换艺术。

一、进制转换的基本原理
1. 二进制与八进制的基本概念
二进制,简而言之,是一种以2为基数的计数系统,使用0和1两个数字符号。在计算机科学中,二进制是数据存储和处理的基础,因为电路的开关状态可以自然地映射到这两个符号上。

八进制,又称八元数制,是一种以8为基数的计数系统,使用0到7共八个数字符号。八进制的一个显著特点是能够紧凑地表示二进制数,每三位二进制数恰好可以对应一个八进制数,这使得在手动计算或表示长二进制数时更加简便。

2. 进制转换的必要性
在计算机科学和数字电路设计中,进制转换是不可或缺的技能。对于开发者而言,理解不同进制间的转换不仅能提高工作效率,还能深入理解计算机内部的工作原理。特别是在处理低级编程、内存管理和数据通信等任务时,掌握进制转换至关重要。

二、二进制转换成八进制的详细步骤
1. 直接分组法
将二进制数从右向左每三位一组进行划分,如果最左边不足三位,则向左补零直至满足三位。然后,将每组二进制数转换为对应的八进制数。例如,二进制数1011010转换为八进制数的步骤如下:
将二进制数划分为101 101 0(不足三位补零);
每组二进制数转换为八进制数:101对应5,101对应5,0对应0;
因此,二进制数1011010对应的八进制数为550。
2. 使用权重法
权重法是基于二进制数的每一位在八进制中代表的权重来进行转换的。具体来说,二进制数的最低位(最右边)在八进制中代表2的0次方(即1),次低位代表2的1次方(即2),以此类推,直到最高位代表2的2次方(即4,如果超出三位则进入下一组)。通过计算每位二进制数在其权重下的值,并将这些值相加,即可得到对应的八进制数。例如,二进制数101转换为八进制数的过程如下:
最低位1代表1(2的0次方);
次低位0代表0(2的1次方);
最高位1代表4(2的2次方);
因此,101对应的八进制数为5(1+0+4=5)。
三、八进制转换成二进制的详细步骤
1. 直接展开法
将八进制数的每一位转换为对应的三位二进制数。由于八进制数的每一位取值范围是0到7,可以直接通过查找或记忆的方式将每个八进制数字映射到相应的三位二进制数。例如,八进制数531转换为二进制数的步骤如下:
5对应二进制数101;
3对应二进制数011;
1对应二进制数001;
因此,八进制数531对应的二进制数为101011001。
2. 逐位展开法
逐位展开法是基于八进制数的每一位在二进制中的表示来进行转换的。具体来说,八进制数的最低位在二进制中表示为该位的值乘以2的0次方,次低位表示为该位的值乘以2的3次方(因为每组八进制数对应三位二进制数),以此类推。不过,这种方法在实际操作中不如直接展开法直观和简便,因此更常用于理论讲解或特定场景下的计算。
四、进制转换的实际应用
1. 在计算机编程中的应用
在计算机编程中,特别是在低级编程和嵌入式系统开发中,二进制和八进制的转换是常见的任务。例如,在读取或写入内存地址时,常常需要将地址从十六进制转换为二进制或八进制;在处理位操作或位掩码时,也需要深入理解不同进制间的转换关系。
2. 在数据通信中的应用
在数据通信领域,特别是在网络通信和串行通信中,二进制和八进制的转换也发挥着重要作用。例如,在串行通信协议中,经常需要将数据帧从二进制格式转换为八进制或十六进制格式以便于调试和分析;在网络通信协议中,也常常需要将IP地址和MAC地址等从点分十进制或冒分十六进制转换为二进制或八进制形式进行处理。
五、进制转换的数学
- 上一篇: 鳗鱼饭制作全攻略
- 下一篇: 橘红色时尚搭配秘籍,解锁色彩新风尚
-
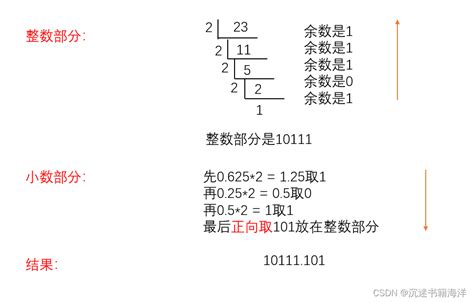 二进制转十进制与十进制转二进制,轻松掌握转换技巧!资讯攻略10-24
二进制转十进制与十进制转二进制,轻松掌握转换技巧!资讯攻略10-24 -
 二进制轻松转换为十进制的方法资讯攻略11-09
二进制轻松转换为十进制的方法资讯攻略11-09 -
 怎样把十进制数转换成二进制形式?资讯攻略10-26
怎样把十进制数转换成二进制形式?资讯攻略10-26 -
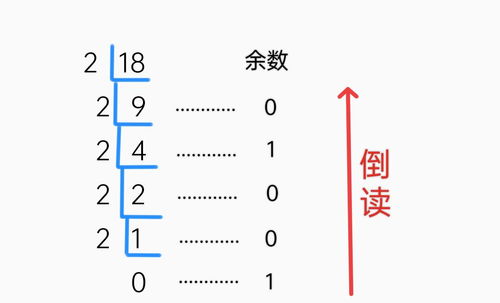 揭秘数字魔法:轻松掌握十进制到二进制的转换秘籍资讯攻略11-04
揭秘数字魔法:轻松掌握十进制到二进制的转换秘籍资讯攻略11-04 -
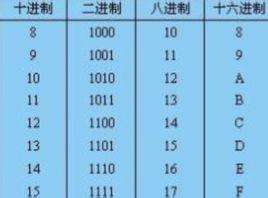 十六进制转换为十进制资讯攻略11-23
十六进制转换为十进制资讯攻略11-23 -
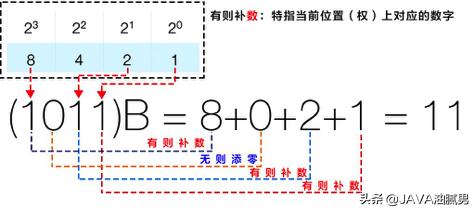 如何将16进制转换为10进制?资讯攻略12-07
如何将16进制转换为10进制?资讯攻略12-07











