如何将16进制转换为10进制？

在日常生活中，我们常常会遇到各种数值表示方式，其中16进制（Hexadecimal）和10进制（Decimal）是两种较为常见的表示方式。尤其在计算机科学、编程和某些专业领域中，16进制的使用非常普遍。本文将详细介绍如何将16进制转换为10进制，旨在让读者能够轻松理解并掌握这一转换方法。

一、了解16进制和10进制的基本概念

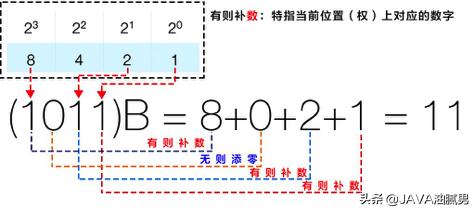
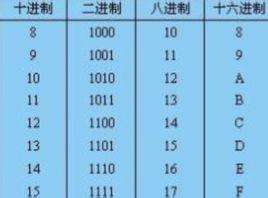
16进制是一种基于16的数值表示方式，使用0-9和A-F这16个符号来表示数值。其中，A代表10，B代表11，C代表12，D代表13，E代表14，F代表15。

10进制是我们日常生活中最为熟悉的数值表示方式，也称为阿拉伯数字，基于10，使用0-9这10个符号表示数值。

二、为什么要进行16进制到10进制的转换

在计算机科学中，16进制被广泛应用，主要有以下几个原因：

1. 便于表示字节：计算机内部以字节为单位存储数据，每个字节由8位二进制数组成。由于2的4次方等于16，所以使用16进制可以非常简洁地表示字节的二进制数值。

2. 缩短表示长度：相比于二进制，16进制使用更少的符号可以表示相同的数据范围，从而简化了阅读和书写。

3. 减少出错率：在进行手动计算或编写代码时，使用16进制可以更容易地进行检查和调试。

然而，在日常生活中，我们通常使用10进制进行计算和交易，所以了解如何将16进制转换为10进制就显得尤为重要。

三、16进制到10进制的转换方法

方法一：按位展开法

1. 逐位写权值：将16进制的每一位从左到右按位权值写下来，最高位（最左边）的权值为16的（位数-1）次方，依次递减。例如，对于16进制数`1A3F`，权值分别为`16^3=4096`、`16^2=256`、`16^1=16`、`16^0=1`。

2. 按位计算：将每一位的数值与其对应的权值相乘，得到每一位的贡献值。例如，`1*4096=4096`、`A*256=10*256=2560`、`3*16=48`、`F*1=15*1=15`。

3. 求和：将所有贡献值相加，得到最终的10进制数。例如，`4096+2560+48+15=6719`。

所以，16进制数`1A3F`转换为10进制数为`6719`。

方法二：逐位直接转换法

这种方法适合熟练掌握16进制与10进制对应关系的读者，步骤相对简单，但需要一定的记忆。

1. 分解16进制数：将16进制数从右到左分解，每一位都是0-9或A-F。

2. 逐位转换：直接将每一位转换为对应的10进制数。

3. 组合：按权值从低位到高位进行组合，得到一个长数字，即转换后的10进制数。

例如，对于16进制数`1A3F`：

`F` 转换为10进制为 `15`

`3` 转换为10进制为 `3`

`A` 转换为10进制为 `10`

`1` 转换为10进制为 `1`

按权值组合后的数字为：`1*4096 + 10*256 + 3*16 + 15*1 = 6719`

这种方法的关键在于能够快速将16进制符号转换为10进制数，并且熟悉位权值的概念。

四、常见技巧与注意事项

1. 快速记忆16进制符号：16进制中的A-F对应的10进制数为10-15，可以简单记忆为字母表中的位置加上9（即A=10，B=11，...，F=15）。

2. 科学计算器辅助：现代的计算器或编程软件通常具备数值转换功能，可以通过科学计算器直接将16进制数转换为10进制数，既快捷又准确。

3. 位权值的应用：在进行按位展开法时，理解并准确计算位权值是转换成功的关键。例如，16进制数中的每一位向左移动一位，相当于其数值乘以16。

4. 手动练习：通过多次手动练习，可以增强对16进制到10进制转换方法的熟练度和准确度。可以尝试使用一些包含复杂16进制数的练习题，进行验证和反思。

五、实际应用举例

在编程中，我们经常需要将颜色值从16进制转换为10进制，例如表示RGB颜色值。例如，红色（RGB：FF0000）在16进制中用`FF0000`表示，其中`FF`表示红色分量，`00`表示绿色分量，`00`表示蓝色分量。将这些分量分别转换为10进制数：

`FF` 转换为10进制为 `255`

`00` 转换为10进制为 `0`

`00` 转换为10进制为 `0`

因此，红色的RGB值为（255, 0, 0）。

在调试时，通过读取内存地址的16进制值，转换为10进制可以更直观地理解地址和存储内容。例如，读取到一个内存地址`0x1A3F`，通过转换我们可以知道它的10进制地址是`6719`。

六、总结

本文详细介绍了16进制转换为10进制的两种方法：按位展开法和逐位直接转换法，同时给出了转换过程中需要注意的常见技巧和实际应用场景。掌握这些转换方法对于计算机科学的学习和应用至关重要，不仅可以提高阅读和理解代码的能力，还能在处理数据时更加高效和准确。

通过阅读本文，相信读者已经对16进制转换为10进制有了全面的理解和把握，可以自如地在不同的数值表示方式之间进行转换，从而在专业领域和个人生活中获得更好的体验。