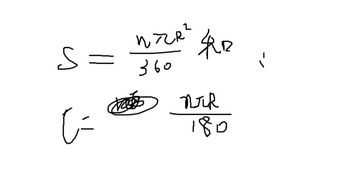揭秘:轻松掌握圆的周长计算方法
在数学的浩瀚宇宙中,圆,这个古老而完美的几何图形,自古以来就与人类的生活和文明紧密相连。从车轮的转动到天体的运行,圆的身影无处不在,而圆的周长,作为衡量这一完美形态外边界长度的关键量,更是承载着丰富的数学原理与实际应用价值。本文将从定义解析、历史沿革、计算方法、实际应用以及现代视角下的圆周率探索等多个维度,深入探讨如何计算圆的周长。
定义解析:何为圆的周长?
圆,是一个平面上所有与给定点(称为圆心)距离相等的点的集合。这个给定的距离,我们称之为半径,记作r。圆的周长,则是围成这个圆的线的长度,通常用大写字母C表示。直观上,我们可以想象用一个无弹性的细绳沿着圆的外边缘环绕一圈,然后拉直测量其长度,这个长度就是圆的周长。

历史沿革:人类对圆周的探索
人类对圆周长的认识与探索,几乎与文明的发展同步。早在公元前3世纪,古希腊数学家阿基米德就通过“逼近法”来估算圆的周长。他首先将圆分成若干等份,然后用多边形的周长来逼近圆的周长。随着分割的份数越来越多,多边形越来越接近圆,其周长也就越来越接近圆的真实周长。阿基米德的工作奠定了圆周率π(圆周长与直径之比)研究的基础。

在中国,南北朝时期的数学家祖冲之,在公元5世纪就精确地计算出了π的值,在3.1415926和3.1415927之间,这一成就比欧洲早了大约一千年。祖冲之的计算方法虽已失传,但他的成果显示了古代中国在数学领域的卓越贡献。
计算方法:从传统到现代的演变
直接测量法
对于较小的圆,可以直接用细绳环绕一圈,然后测量绳子的长度。这种方法简单直观,但精度受限于测量工具的精度和人为操作的误差。
公式计算法
随着数学的发展,人们发现了计算圆周长的精确公式:C = 2πr 或 C = πd(d为直径)。这个公式简洁而优雅,将圆的周长与半径或直径直接联系起来,但关键在于准确知道π的值。
数值逼近法
在实际应用中,由于π是一个无理数,无法精确表示为一个有限小数或分数,因此常常采用数值逼近的方法来计算圆的周长。除了阿基米德的多边形逼近法外,还有莱布尼茨的级数求和法、牛顿的迭代法等,这些方法虽然复杂,但能提供高精度的π值,从而准确计算圆的周长。
实际应用:圆周长的广泛影响
圆的周长不仅仅是一个数学概念,它在日常生活中有着广泛的应用。
车轮与交通:车轮的设计直接依赖于圆的周长,因为它决定了车轮每转一圈所覆盖的距离。汽车轮胎的周长对计算车速、里程至关重要。
建筑与设计:在建筑设计中,圆弧形结构如拱门、穹顶等,其尺寸的计算往往涉及到圆周长的计算,确保结构的稳定与美观。
电子工程:在通信领域,信号的波长(一种周期性的波动,其长度类似于圆的周长)是决定信号传输特性的关键因素之一。
天文学:行星绕恒星的运动轨迹可以视为椭圆(在极端情况下接近圆),通过计算其“周长”(即轨道长度),可以预测天体的运动规律。
现代视角下的圆周率探索
随着科技的发展,人类对π的探索进入了一个全新的阶段。计算机的出现,使得人们能够以前所未有的精度计算π的值。目前,π的已知位数已超过数十万亿位,这一成就不仅展示了现代计算技术的强大,也促进了数学、物理学等多个领域的研究。
在理论研究方面,π的无限不循环小数特性,成为了研究实数结构、数论、复分析等领域的重要对象。一些数学家甚至提出,π中可能隐藏着宇宙的所有秘密,这一观点虽然带有哲学色彩,但无疑激发了人们对π及其背后数学原理的无限遐想。
此外,π的计算也成为了检验计算机性能的一项基准测试。高效、快速地计算π,不仅能够推动算法设计与优化,还能促进计算机科学本身的发展。
结语
圆的周长,作为连接数学与现实的桥梁,不仅承载了人类对美的追求,也体现了人类对未知的探索精神。从古至今,无数数学家、科学家为之付出了智慧与汗水,他们的努力不仅推动了数学理论的发展,也为人类社会的进步做出了不可磨灭的贡献。如今,随着科技的进步,我们对圆的周长、对π的理解正不断深化,而这些知识,正如同圆本身一样,无限延伸,永无止境。在探索的道路上,人类将继续前行,用智慧与好奇心,解锁更多关于圆的奥秘,让数学的光芒照亮人类的未来。
- 上一篇: 轻松学会!用纸条编织浪漫心形教程
- 下一篇: 东北三省的总面积是多少?
-
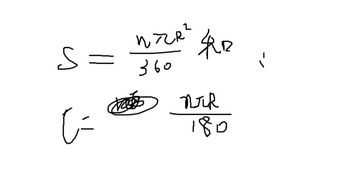 如何计算扇形的周长?资讯攻略11-18
如何计算扇形的周长?资讯攻略11-18 -
 揭秘长方体周长:轻松掌握计算公式资讯攻略11-13
揭秘长方体周长:轻松掌握计算公式资讯攻略11-13 -
 圆周率的计算方法详解资讯攻略11-15
圆周率的计算方法详解资讯攻略11-15 -
 揭秘圆周率:探寻隐藏的数学奥秘与规律资讯攻略11-19
揭秘圆周率:探寻隐藏的数学奥秘与规律资讯攻略11-19 -
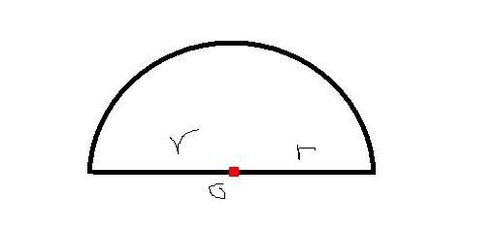
 六年级学生必知的半圆周长计算公式资讯攻略11-10
六年级学生必知的半圆周长计算公式资讯攻略11-10 -
 揭秘长方体周长计算的奥秘公式资讯攻略11-14
揭秘长方体周长计算的奥秘公式资讯攻略11-14