如何计算扇形的周长?
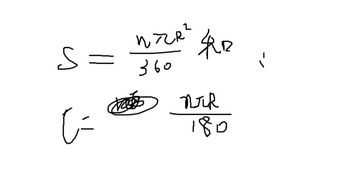
在我们丰富多彩的几何世界里,扇形以其独特的形状和广泛的应用而备受瞩目。无论是在建筑设计、艺术创作,还是在数学学习中,扇形都扮演着重要的角色。然而,对于扇形的周长计算,很多人可能会感到困惑。别担心,今天我们就来揭开扇形周长的神秘面纱,让你轻松掌握这一计算技巧。

首先,让我们来了解一下扇形的基本概念。扇形是圆的一部分,由两条半径和圆上的一段弧组成。它就像是一个被切开的圆饼,既保留了圆的柔美线条,又增添了独特的几何美感。扇形的周长,顾名思义,就是围绕扇形边缘一圈的长度。这个周长由扇形的两个半径和弧长共同构成。

那么,如何计算扇形的周长呢?这就涉及到一些基本的几何知识和公式了。首先,我们需要知道圆的周长公式,即C=2πr,其中C代表圆的周长,r代表圆的半径。这个公式是计算扇形弧长的基础。

接下来,我们要引入扇形弧长的计算公式。扇形弧长是圆周长的一部分,具体占多少比例,取决于扇形的圆心角。圆心角是扇形顶点与圆心连线的夹角,通常用θ表示,单位为弧度或度。在弧度制下,扇形弧长L的计算公式为L=θr,其中θ为圆心角的弧度值,r为圆的半径。这个公式告诉我们,扇形弧长与圆心角的弧度值和半径成正比。
现在,我们已经有了计算扇形弧长的工具,接下来就可以求解扇形的周长了。扇形的周长P由两个半径和一个弧长组成,因此可以表示为P=2r+L。将扇形弧长的计算公式代入,得到P=2r+θr。这个公式简洁明了,只需要知道扇形的半径和圆心角的弧度值,就可以轻松计算出扇形的周长了。
不过,在实际应用中,我们经常会遇到圆心角以度为单位的情况。这时,我们需要将圆心角的度数转换为弧度值,才能使用上述公式进行计算。圆心角的弧度值与度数之间的转换公式为θ(弧度)=θ(度)×π/180。通过这个公式,我们可以将任何以度为单位的圆心角转换为弧度值,进而计算扇形的周长。
为了更直观地理解扇形周长的计算过程,让我们来看一个具体的例子。假设有一个扇形,其半径为5厘米,圆心角为90度。我们要求这个扇形的周长。
首先,我们需要将圆心角的度数转换为弧度值。根据转换公式,θ(弧度)=90×π/180=π/2。
然后,我们将转换后的弧度值和半径代入扇形周长的计算公式中。得到P=2r+θr=2×5+(π/2)×5=10+(5/2)π≈10+7.85=17.85(厘米)。
通过这个例子,我们可以看到扇形周长的计算过程并不复杂。只要掌握了基本的几何知识和公式,就可以轻松应对各种扇形周长的计算问题。
当然,除了上述的基本计算方法外,扇形周长还有一些其他的求解方式。例如,我们可以利用扇形的面积和圆心角来求解周长。扇形的面积公式为S=(1/2)θr²,其中θ为圆心角的弧度值,r为圆的半径。通过扇形面积和圆心角,我们可以推导出扇形的弧长,进而求解周长。不过,这种方法相对复杂一些,需要一定的数学基础和推导能力。
此外,扇形周长还可以与三角函数相结合进行计算。在某些特殊情况下,我们可以利用三角函数来求解扇形的半径或圆心角,进而计算周长。这种方法虽然灵活多变,但也需要对三角函数有深入的理解和掌握。
总的来说,扇形周长的计算是一个既基础又重要的几何问题。它涉及到圆的周长、扇形弧长、圆心角等多个几何概念,是检验我们几何知识和计算能力的一个好题目。通过学习和掌握扇形周长的计算方法,我们可以更好地理解几何图形的性质和关系,提高我们的数学素养和解题能力。
在日常生活中,扇形周长的计算也有着广泛的应用。比如,在建筑设计中,我们需要计算扇形窗户或门的周长,以确定所需的材料和尺寸;在艺术创作中,我们需要根据扇形的周长来绘制或裁剪出合适的形状;在数学学习中,扇形周长的计算更是我们理解和掌握几何知识的重要一环。
因此,我们应该重视扇形周长的计算问题,努力提高自己的计算能力和几何素养。通过不断的学习和实践,我们可以逐渐掌握扇形周长的计算技巧和方法,更好地应对各种几何问题和挑战。
最后,让我们再次回顾一下扇形周长的计算公式:P=2r+θr。这个公式简洁而有力,它告诉我们扇形的周长与半径和圆心角的弧度值密切相关。只要掌握了这个公式和相关的几何知识,我们就可以轻松应对各种扇形周长的计算问题了。
希望这篇文章能够帮助你更好地理解扇形周长的计算方法和技巧。在未来的学习和生活中,愿你能够运用所学的几何知识去探索和发现更多的数学奥秘!
- 上一篇: 如何使用刻录机?
- 下一篇: 家常豆花DIY:一步步教你轻松制作
-
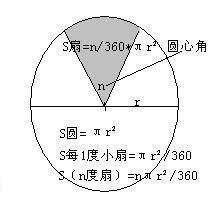 扇形的所有重要公式汇总资讯攻略10-28
扇形的所有重要公式汇总资讯攻略10-28 -
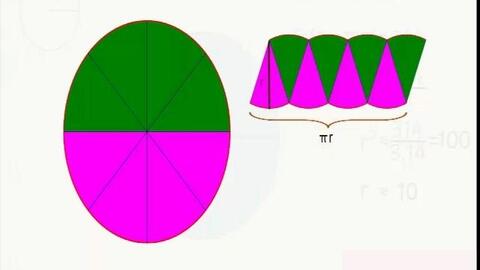 扇形面积如何计算?资讯攻略11-27
扇形面积如何计算?资讯攻略11-27 -
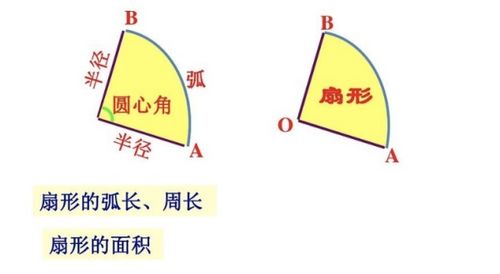 揭秘扇形弧长的计算方法,轻松掌握几何奥秘!资讯攻略11-19
揭秘扇形弧长的计算方法,轻松掌握几何奥秘!资讯攻略11-19 -
 三角形周长计算:使用周长公式的方法资讯攻略11-11
三角形周长计算:使用周长公式的方法资讯攻略11-11 -
 揭秘长方体周长:轻松掌握计算公式资讯攻略11-13
揭秘长方体周长:轻松掌握计算公式资讯攻略11-13 -
 高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08
高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08












