揭秘:凸四边形与凹四边形,你真的了解它们的定义吗?
在几何学中,四边形是一个重要的基本形状,它拥有四条边和四个顶点。根据边和顶点的相对位置关系,四边形可以进一步细分为凸四边形和凹四边形。这两种四边形在定义、性质以及应用场景上都有着显著的差异。

首先,我们来看凸四边形的定义。凸四边形是指所有内角均小于180度的四边形。换句话说,如果一个四边形的所有顶点都位于其任意一边的同一侧(即不存在一个顶点使得连接该顶点与其他三个顶点的线段中有一条穿过四边形的内部),那么这个四边形就是凸四边形。常见的凸四边形有正方形、矩形、菱形、平行四边形、梯形等。凸四边形的一个重要性质是其所有内角之和等于360度,这是多边形内角和公式的一个特例。此外,凸四边形的对角线互相平分(仅对平行四边形而言,其他凸四边形不一定具备此性质),且任意两边之和大于第三边,任意两边之差小于第三边,这些性质都是基于三角形的基本性质推导出来的。
正方形作为凸四边形的一种特殊形式,其四条边等长且四个内角均为直角。矩形则具有对边平行且等长,以及四个内角均为直角的性质。菱形则要求四条边等长,但其内角不一定为直角。平行四边形则是一个更一般的概念,它要求两组对边分别平行且等长,但内角和边长可以变化。梯形则要求只有一组对边平行,这组平行的对边被称为梯形的上底和下底,而不平行的两边则被称为梯形的腰。

接下来,我们讨论凹四边形的定义。与凸四边形相反,凹四边形是指至少存在一个内角大于或等于180度的四边形。换句话说,如果一个四边形存在一个顶点,使得连接该顶点与其他三个顶点的线段中至少有一条穿过四边形的内部,那么这个四边形就是凹四边形。凹四边形在日常生活中可能不如凸四边形常见,但它们在几何学和图形学中仍然有着重要的应用。
凹四边形的一个显著特点是其内角之和可能大于360度。这是因为凹四边形中存在至少一个反射角(即大于180度的内角),这个反射角会使得四边形的内角之和增加。此外,凹四边形的对角线不一定互相平分,也不一定满足三角形的基本不等式(任意两边之和大于第三边,任意两边之差小于第三边)。这些性质使得凹四边形在几何学中具有独特的地位。
为了更直观地理解凸四边形和凹四边形的区别,我们可以考虑一些具体的例子。例如,一个普通的矩形窗户可以看作是一个凸四边形,因为它的所有内角都小于180度,且所有顶点都位于其任意一边的同一侧。而一个凹陷的墙角则可以看作是一个凹四边形,因为它存在一个内角大于180度,且这个内角所在的顶点会使得连接该顶点与其他三个顶点的线段中有一条穿过四边形的内部。
在实际应用中,凸四边形和凹四边形都有着广泛的应用。在建筑设计中,凸四边形常被用作窗户、门洞等结构的基本形状,因为它们具有简洁、美观且易于加工的特点。而凹四边形则可能在一些特殊的建筑设计中出现,如凹陷的墙角、拱形门等,这些设计不仅具有美学价值,还可能具有特定的功能需求(如提供更好的遮阳效果、增强结构的稳定性等)。
在图形学和计算机视觉领域,凸四边形和凹四边形的识别和处理也是重要的研究内容。例如,在计算机辅助设计中,软件需要能够自动识别并处理各种形状的四边形,以便进行精确的尺寸测量、形状优化等操作。在这个过程中,区分凸四边形和凹四边形是非常重要的,因为它们的处理方法和应用场景往往不同。
此外,在机器人导航、图像处理等领域,凸四边形和凹四边形的识别也具有重要的应用价值。例如,在机器人导航中,机器人需要能够识别并避开障碍物,而障碍物往往可以看作是由各种形状的四边形(包括凸四边形和凹四边形)组成的。通过识别这些四边形的形状和位置关系,机器人可以制定出更加精确的导航策略。
综上所述,凸四边形和凹四边形是几何学中两个重要的概念。它们不仅具有独特的定义和性质,还在建筑设计、图形学、计算机视觉等领域有着广泛的应用。通过深入研究这两种四边形的特点和性质,我们可以更好地理解它们在实际应用中的价值和意义,从而为相关领域的发展提供有力的支持。
- 上一篇: 小米商城直播观看指南
- 下一篇: 如何轻松设置苹果手机的个性化闹钟铃声?
-
 探索四边形世界的奥秘资讯攻略11-04
探索四边形世界的奥秘资讯攻略11-04 -
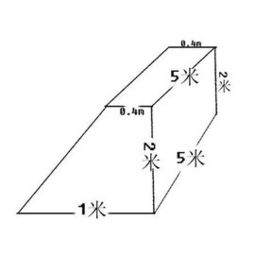 揭秘梯形体积计算的神秘公式!资讯攻略11-10
揭秘梯形体积计算的神秘公式!资讯攻略11-10 -
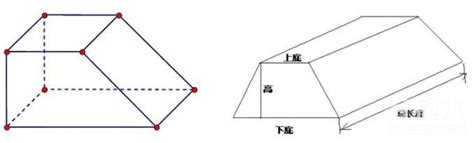 揭秘梯形体积计算:轻松掌握公式秘籍资讯攻略10-30
揭秘梯形体积计算:轻松掌握公式秘籍资讯攻略10-30 -
 解锁初中数学奥秘:不可不知的48个关键几何模型全揭秘!资讯攻略12-08
解锁初中数学奥秘:不可不知的48个关键几何模型全揭秘!资讯攻略12-08 -
 揭秘:公斤与KG的等同关系,你真的了解吗?资讯攻略11-30
揭秘:公斤与KG的等同关系,你真的了解吗?资讯攻略11-30 -
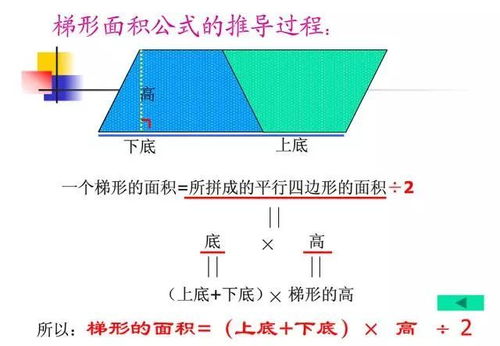 平行四边形与梯形的面积及周长计算公式资讯攻略12-06
平行四边形与梯形的面积及周长计算公式资讯攻略12-06











