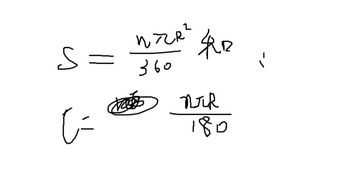扇形面积如何计算?
在探索几何世界的奇妙之旅中,扇形以其独特的形态和广泛的应用,成为了我们不可忽视的一部分。想象一下,无论是精致的蛋糕切片,还是华丽的舞台幕布,甚至是自然界中那缓缓展开的叶片,都蕴含着扇形的魅力。但你是否真正了解,这个看似简单的图形背后,隐藏着怎样的面积计算奥秘呢?今天,就让我们一起揭开扇形面积计算的神秘面纱,走进一个既实用又充满趣味的知识殿堂。
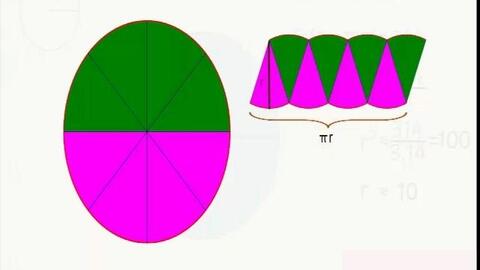
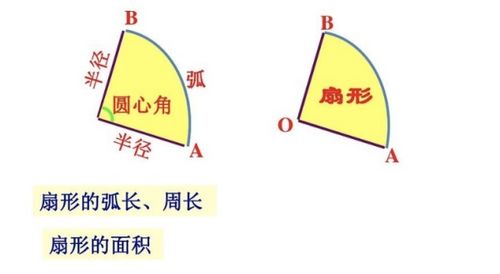
首先,让我们从基础出发,明确什么是扇形。扇形,简单来说,就是圆的一部分,它被两条半径和圆上的一段弧所围成。就像一个美味的披萨被均匀切分后的每一块,每一块都是一个扇形。那么,如何准确计算出这块“披萨片”的面积呢?
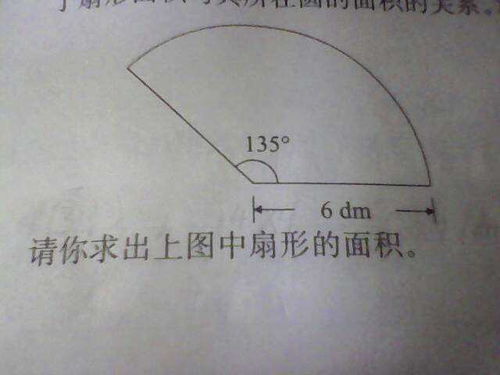
扇形面积的奥秘:从公式出发
扇形面积的计算,离不开一个核心公式——扇形面积 = (圆心角/360°)× π × 半径²。这个公式看似简单,却蕴含了深刻的几何原理。圆心角,顾名思义,就是扇形所对应的圆中心角的大小,通常用度数来表示。而π,这个数学中的神奇常数,约等于3.14159…,它在圆的面积、周长等计算中扮演着至关重要的角色。半径,则是从圆心到圆上任一点的距离,它决定了圆的大小,也直接影响着扇形的面积。

圆心角的秘密
圆心角是扇形面积计算中的关键一环。想象一下,如果一个完整的圆是一个360°的圆舞曲,那么扇形就像是这段舞曲中的一个美妙片段。圆心角越大,扇形所占的比例就越大,面积自然也就越大。反之,圆心角越小,扇形就越“瘦小”,面积也就相应减小。因此,准确测量或知道圆心角的大小,是计算扇形面积的第一步。

π的魔力
π,这个让无数数学家为之痴迷的常数,在扇形面积的计算中同样扮演着举足轻重的角色。它的存在,使得我们能够将圆的周长、面积等复杂问题简化为简单的数学表达式。在扇形面积的计算中,π与半径的平方相乘,再乘以圆心角与360°的比例,就得到了扇形的面积。这个过程中,π就像是一把钥匙,打开了通往扇形面积计算的神秘之门。
半径的力量
如果说圆心角决定了扇形在圆中所占的比例,那么半径则决定了这个比例所对应的具体大小。半径越长,扇形就越大;半径越短,扇形就越小。这就像是吹气球一样,气球的大小(即扇形的面积)与吹入的气量(即半径的平方)成正比。因此,在计算扇形面积时,准确测量或知道半径的长度同样至关重要。
实战演练:扇形面积的计算
掌握了扇形面积的计算公式和基本原理后,接下来就让我们通过几个实例来巩固一下所学知识吧!
示例一:已知圆心角和半径
假设有一个扇形,其圆心角为90°,半径为5厘米。根据扇形面积的计算公式,我们可以得到:
扇形面积 = (90°/360°)× π × 5² = 1/4 × π × 25 ≈ 19.63平方厘米
示例二:已知弧长和半径
有时,我们可能只知道扇形的弧长和半径,而不知道圆心角。这时,我们可以先通过弧长公式反推出圆心角,再计算扇形面积。弧长公式为:弧长 = 圆心角/360° × 2π × 半径。
假设有一个扇形,其弧长为6.28厘米,半径为2厘米。首先,我们通过弧长公式反推出圆心角:
圆心角 = 弧长 / (2π × 半径) × 360° = 6.28 / (2 × π × 2) × 360° = 90°
然后,再根据扇形面积的计算公式得到:
扇形面积 = (90°/360°)× π × 2² = 1/4 × π × 4 ≈ 3.14平方厘米
示例三:扇形在生活中的应用
扇形不仅在数学中有着重要的地位,更在我们的日常生活中有着广泛的应用。比如,在制作蛋糕时,我们常常需要将蛋糕均匀切分成若干份,每一份就是一个扇形。通过计算每份蛋糕的面积,我们可以确保每个人都能得到相同大小的蛋糕块。此外,在建筑设计、机械制造等领域,扇形也经常被用作设计元素或零件形状,其面积的计算对于确保设计的准确性和实用性至关重要。
结语:扇形面积的趣味探索
扇形面积的计算,不仅是一项实用的数学技能,更是一次充满乐趣的几何探索之旅。在这个过程中,我们不仅能够学到如何运用公式解决实际问题,还能深刻体会到数学与生活的紧密联系。无论是制作蛋糕时的精准切割,还是建筑设计中的巧妙构思,扇形都以其独特的魅力,为我们的生活增添了无限的色彩和可能。
所以,下次当你再看到那些精美的扇形图案时,不妨试着用今天学到的知识去计算一下它们的面积吧!相信在这个过程中,你会收获更多的乐趣和成就感。让我们一起,用数学的眼光去发现生活中的美好吧!
- 上一篇: 如何进行比亚迪汽车APP的实名认证
- 下一篇: 酷狗音乐平台上发布个人原创歌曲的秘籍
-
 高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08
高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08 -
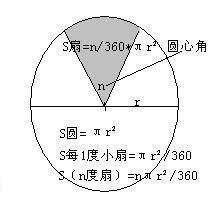 扇形的所有重要公式汇总资讯攻略10-28
扇形的所有重要公式汇总资讯攻略10-28 -
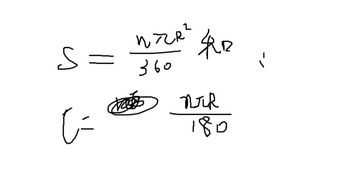 如何计算扇形的周长?资讯攻略11-18
如何计算扇形的周长?资讯攻略11-18 -
 揭秘扇形弧长的计算方法,轻松掌握几何奥秘!资讯攻略11-19
揭秘扇形弧长的计算方法,轻松掌握几何奥秘!资讯攻略11-19 -
 Excel制作扇形统计图教程资讯攻略11-09
Excel制作扇形统计图教程资讯攻略11-09 -
 小学阶段如何绘制扇形统计图资讯攻略11-12
小学阶段如何绘制扇形统计图资讯攻略11-12