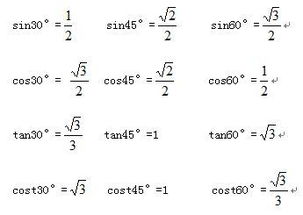三角函数cot的定义及公式是什么?
在数学的海洋中,隐藏着无数令人着迷的公式与定理,它们如同璀璨星辰,指引着求知者探索未知的领域。今天,让我们一同潜入这片深邃的数学宇宙,聚焦于一个既古老又神秘的角色——三角函数中的cot(余切)函数,揭开它神秘的面纱,深入了解三角函数cot的公式及其背后的奥秘。

三角函数cot:一场数学与几何的浪漫邂逅
在数学的殿堂里,三角函数是连接代数与几何的桥梁,它们以独特的方式描述了平面直角坐标系中角度与边长之间的关系。而cot函数,作为三角函数家族中的重要一员,以其独特的性质,在解决几何问题、物理现象乃至工程应用中发挥着不可替代的作用。那么,三角函数cot的公式究竟是什么?它又是如何在数学的舞台上翩翩起舞的呢?
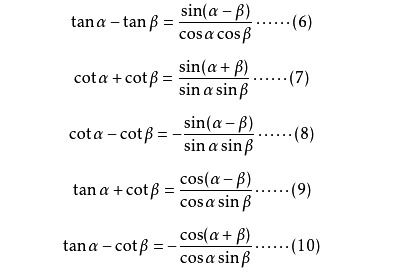
揭开cot的神秘面纱:定义与公式
首先,让我们从cot函数的定义说起。在直角三角形中,任意一锐角的余切值定义为该角的邻边长度与对边长度之比,用数学符号表示为:cotθ = 邻边/对边。这里的θ代表直角三角形中的一个锐角,而邻边和对边则是相对于这个角而言的两条直角边。

然而,这只是cot函数在直角三角形中的直观表达。在更广泛的数学领域,cot函数有着更为通用的定义。在任意角θ(θ ≠ kπ, k为整数)的情况下,cotθ可以通过正弦函数sinθ和余弦函数cosθ的比值来定义,即cotθ = cosθ/sinθ。这个公式不仅适用于锐角,也适用于钝角、直角(需通过极限概念理解)以及任意角度的终边落在坐标轴上的特殊情况。

深入探索:cot函数的性质与应用
了解了cot函数的定义后,我们不禁要问,这个函数究竟有哪些独特的性质?它又能解决哪些实际问题呢?
性质一:周期性
cot函数是一个周期函数,其周期为π。这意味着,对于任意整数k,cot(θ + kπ) = cotθ。这一性质使得cot函数在图形上呈现出周期性的波动,为我们在解决周期性问题时提供了便利。
性质二:奇偶性
cot函数是奇函数,即cot(-θ) = -cotθ。这一性质揭示了cot函数在正负角度之间的对称性,有助于我们简化计算和理解函数图像。
性质三:渐近线
cot函数的图像在θ = kπ(k为整数)处存在垂直渐近线。这意味着,当θ趋近于这些值时,cotθ的绝对值将趋于无穷大。这一性质在解决涉及cot函数的极限问题时尤为重要。
应用一:几何问题
在几何学中,cot函数常用于解决与直角三角形相关的角度和边长问题。例如,在测量、建筑和导航等领域,cot函数可以帮助我们确定物体的倾斜角度或计算两点间的距离。
应用二:物理现象
在物理学中,cot函数也扮演着重要角色。例如,在波动理论、光学和电磁学中,cot函数常用于描述波的传播特性、光的折射和反射规律以及电磁场的分布等。
应用三:工程应用
在工程领域,cot函数同样有着广泛的应用。例如,在信号处理、控制系统和通信网络中,cot函数可以帮助我们分析和设计系统的稳定性和性能。
实战演练:cot公式的应用实例
理论终归要付诸实践。接下来,让我们通过几个实例来感受cot公式的魅力。
实例一:求解直角三角形中的角度
已知直角三角形的邻边长为3,对边长为4,求锐角的余切值及该角的度数。
解:根据cot函数的定义,cotθ = 邻边/对边 = 3/4。然后,利用反余切函数(arccot)求解θ,得到θ ≈ 36.87°(注意,这里的结果为近似值,实际计算中可能需要使用计算器或查表得到精确值)。
实例二:分析物理波动
考虑一个简谐振动系统,其位移y随时间t的变化关系为y = A * cot(ωt + φ),其中A为振幅,ω为角频率,φ为初相位。分析该系统在不同时间点的位移情况。
解:根据cot函数的周期性,我们知道系统将在每个π/ω的时间间隔内重复其振动模式。此外,利用cot函数的渐近线性质,我们可以确定系统在t = (kπ - φ)/ω(k为整数)时达到极值(最大或最小位移)。
实例三:工程设计中的稳定性分析
在控制系统设计中,我们可能需要分析一个系统的稳定性。假设系统的特征方程为s^2 + 2s + cot(α) = 0,其中α为系统参数。分析α的取值对系统稳定性的影响。
解:首先,我们注意到cot(α)在α = kπ(k为整数)处存在垂直渐近线。这意味着,当α接近这些值时,系统的特征根将趋于无穷大,导致系统不稳定。因此,在设计控制系统时,我们需要避免α取这些值以确保系统的稳定性。
结语:cot函数——数学之美的缩影
通过上述探讨,我们不难发现,cot函数不仅是三角函数家族中的一位重要成员,更是连接数学与现实生活的一座桥梁。它以其独特的定义、性质和广泛的应用,展现了数学之美与实用性的完美结合。无论是解决几何问题、分析物理现象还是进行工程设计,cot函数都以其独特的魅力,引领着我们探索未知、创造未来。
在数学的世界里,每一个公式、每一个定理都是人类智慧的结晶。它们不仅揭示了自然界的奥秘,也为我们提供了解决问题的工具和方法。因此,让我们继续在数学的海洋中遨游,不断发现新的宝藏,共同书写人类文明的辉煌篇章。
- 上一篇: 《别惹佐汉》:解锁影片中所有动人心弦的歌曲
- 下一篇: 如何在抖音中设置字体大小?
-
 cot导数的定义与计算方法资讯攻略11-24
cot导数的定义与计算方法资讯攻略11-24 -
 余切公式具体是指什么?资讯攻略11-08
余切公式具体是指什么?资讯攻略11-08 -
 三角函数常见公式都有哪些?资讯攻略11-28
三角函数常见公式都有哪些?资讯攻略11-28 -
 棱锥体积公式详解,轻松掌握!资讯攻略10-30
棱锥体积公式详解,轻松掌握!资讯攻略10-30 -
 高中数学必备:三角函数公式全集(终极版)资讯攻略11-30
高中数学必备:三角函数公式全集(终极版)资讯攻略11-30 -
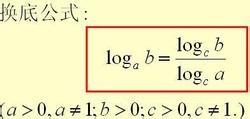 对数基本公式:详解log函数的定义与应用资讯攻略10-26
对数基本公式:详解log函数的定义与应用资讯攻略10-26