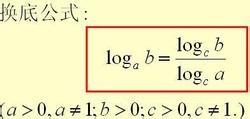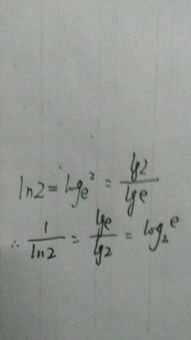掌握log函数求导公式,轻松解决数学问题
探索数学之美:log函数的求导公式全解析
在数学的广阔天地里,导数如同一把神奇的钥匙,为我们打开了探索函数性质的大门。无论是物理学家研究运动规律,经济学家分析市场趋势,还是工程师设计复杂系统,导数都扮演着不可或缺的角色。而log函数,作为数学中的一位“老熟人”,不仅频繁出现在各种科学计算和工程应用中,其求导过程更是充满了智慧与技巧。今天,就让我们一起踏上这段探索之旅,揭开log函数求导公式的神秘面纱。
一、初识log函数
log函数,即对数函数,是对数的逆运算。简单来说,如果我们知道某个数的对数是多少,就可以通过这个对数“还原”出原来的数。在数学上,log函数有多种底数形式,最常见的是以e(自然对数的底,约等于2.71828)为底的自然对数ln(x),以及以10为底的常用对数log10(x)(有时简写为log(x))。
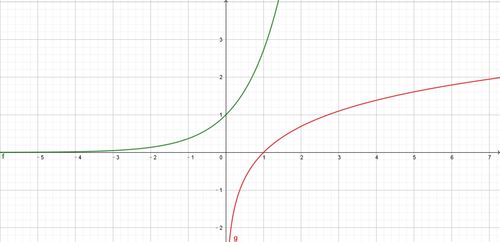
对数函数的图像呈现出优美的S形曲线,它们不仅在数学上有着广泛的应用,还是连接微积分、概率论、信息论等多个数学分支的桥梁。那么,如此重要的log函数,其导数会是怎样的呢?
二、导数基础回顾
在深入探讨log函数的求导之前,让我们先回顾一下导数的基本概念。导数,简单来说,就是函数在某一点的变化率。它描述了函数值随着自变量变化的快慢程度。对于函数f(x),其在x0点的导数记为f'(x0),可以通过极限的方式定义:
f'(x0) = lim (Δx→0) [f(x0+Δx) - f(x0)] / Δx
这个定义虽然抽象,但它揭示了导数计算的本质——求极限。在实际操作中,我们常常通过已知的导数公式或求导法则来计算复杂函数的导数。
三、log函数的求导公式
现在,我们终于来到了log函数求导的核心部分。对于自然对数函数ln(x),其导数公式为:
(ln(x))' = 1/x
这个公式简洁而优美,它告诉我们,自然对数函数在其定义域(0, +∞)内的每一点上,其变化率都与该点的函数值成反比。
对于常用对数函数log10(x),其导数可以通过自然对数函数的导数公式进行转换。我们知道,log10(x) = ln(x) / ln(10),因此:
(log10(x))' = [ln(x) / ln(10)]' = (1/ln(10)) * (ln(x))' = (1/ln(10)) * (1/x) = 1/(x * ln(10))
同样地,这个公式也揭示了常用对数函数在其定义域内的变化率特性。
四、求导公式的证明
虽然我们已经知道了log函数的求导公式,但知其然更要知其所以然。接下来,我们简要证明一下自然对数函数ln(x)的导数公式。
考虑函数y = ln(x),我们希望找到这个函数的导数y'。根据导数的定义,我们有:
y' = lim (Δx→0) [ln(x+Δx) - ln(x)] / Δx
为了简化这个极限表达式,我们可以利用对数函数的性质进行转换。注意到ln(a/b) = ln(a) - ln(b),我们可以将上式重写为:
y' = lim (Δx→0) ln[(x+Δx)/x] / Δx
接下来,我们利用等价无穷小的概念。当Δx→0时,(x+Δx)/x - 1 → 0,且ln(1+u)与u是等价无穷小(当u→0时)。因此,我们可以将上式进一步化简为:
y' = lim (Δx→0) [(x+Δx)/x - 1] / Δx * lim (u→0) ln(1+u) / u
由于lim (u→0) ln(1+u) / u = 1(这是自然对数函数在u=0点处的导数),我们可以将上式中的第二个极限值替换为1,得到:
y' = lim (Δx→0) [(x+Δx)/x - 1] / Δx = lim (Δx→0) Δx / [x * Δx] = 1/x
这样,我们就证明了自然对数函数ln(x)的导数公式。对于常用对数函数log10(x)的导数公式,其证明过程类似,只是需要额外利用对数换底公式进行转换。
五、应用实例与
- 上一篇: 如何在便签Tips中添加待办事项?
- 下一篇: 手机屏幕分辨率有哪三种?一文带你全面了解!
-
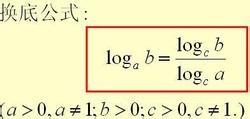 对数基本公式:详解log函数的定义与应用资讯攻略10-26
对数基本公式:详解log函数的定义与应用资讯攻略10-26 -
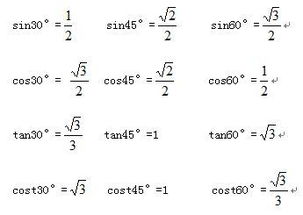 三角函数常见公式都有哪些?资讯攻略11-28
三角函数常见公式都有哪些?资讯攻略11-28 -
 高中数学必备:三角函数公式全集(终极版)资讯攻略11-30
高中数学必备:三角函数公式全集(终极版)资讯攻略11-30 -
 揭秘:log函数的定义域究竟隐藏着什么奥秘?资讯攻略11-23
揭秘:log函数的定义域究竟隐藏着什么奥秘?资讯攻略11-23 -
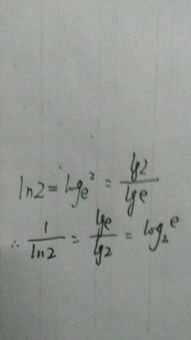 揭秘:log2到底是什么?一文读懂!资讯攻略11-10
揭秘:log2到底是什么?一文读懂!资讯攻略11-10 -
 三角函数cot的定义及公式是什么?资讯攻略11-24
三角函数cot的定义及公式是什么?资讯攻略11-24