气体摩尔体积的定义及公式
在化学的世界里,有一个非常实用的概念叫做“气体摩尔体积”,它能够帮助我们理解气体的性质和行为。想象一下,你手里有一瓶气体,无论是氢气、氧气还是氮气,我们都可以用一个简单的公式来描述这些气体在一定条件下的体积。这个公式就是气体摩尔体积公式,它不仅可以用于计算,还能帮助我们理解气体的一些基本特性。接下来,我们就来详细探讨一下这个公式是什么,以及它是怎么来的,还有它的实际应用。
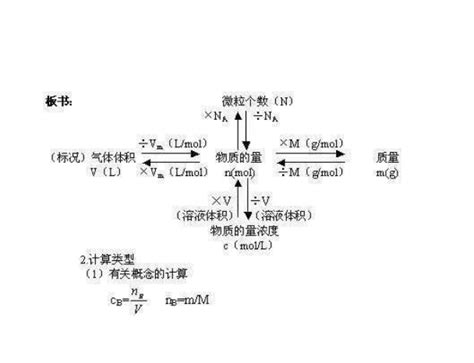
首先,我们需要知道什么是摩尔。摩尔是化学中的一个基本单位,它表示的是物质中粒子的数量。具体来说,1摩尔的任何物质都包含有相同数目的基本单位(如原子、分子或离子),这个数目大约是6.022×10^23个,被称为阿伏伽德罗常数。这个概念很重要,因为它让我们能够用相同的标准去衡量不同物质的量。

那么,气体摩尔体积是什么呢?气体摩尔体积是指在一定的温度和压强下,1摩尔气体所占的体积。也就是说,如果我们知道了某种气体在一定条件下的气体摩尔体积,就可以计算出1摩尔这种气体的体积是多少。这个值并不是固定的,它会随着温度和压强的变化而变化。
接下来,我们就来介绍一下气体摩尔体积的公式。在标准状况下(即温度为0摄氏度,压强为101.325千帕),气体摩尔体积的值约为22.4升/摩尔。所以,气体摩尔体积公式可以表示为:
V = n × Vₘ
其中,V表示气体的总体积(单位:升),n表示气体的物质的量(单位:摩尔),Vₘ表示气体摩尔体积(在标准状况下约为22.4升/摩尔)。
这个公式很简单,但它非常有用。比如,如果我们知道了一定量的气体的物质的量,就可以用这个公式来计算出它在标准状况下的体积。反过来,如果我们知道了气体的体积和气体摩尔体积,也可以用这个公式来计算出气体的物质的量。
不过,需要注意的是,这个公式只适用于标准状况下的气体。如果在其他温度和压强下,我们就需要使用更一般的公式来计算气体摩尔体积。这个公式叫做理想气体状态方程,它表示的是气体的压强、体积、温度和物质的量之间的关系。理想气体状态方程可以表示为:
pV = nRT
其中,p表示气体的压强(单位:帕斯卡),V表示气体的体积(单位:立方米),n表示气体的物质的量(单位:摩尔),R表示理想气体常数(约为8.314焦耳/(摩尔·开尔文)),T表示气体的热力学温度(单位:开尔文)。
通过理想气体状态方程,我们可以推导出在任意温度和压强下的气体摩尔体积公式。将理想气体状态方程改写为:
Vₘ = V / n = RT / p
其中,Vₘ表示气体摩尔体积(单位:立方米/摩尔)。这个公式告诉我们,气体摩尔体积与气体的压强成反比,与气体的热力学温度成正比。也就是说,当压强增大时,气体摩尔体积会减小;当温度升高时,气体摩尔体积会增大。
那么,为什么气体摩尔体积会随着温度和压强的变化而变化呢?这是因为气体分子之间的距离很大,分子间的相互作用力很弱。因此,当温度升高时,气体分子的热运动会加剧,分子间的平均距离会增大,从而导致气体体积增大;而当压强增大时,气体分子会受到更大的压力作用,分子间的平均距离会减小,从而导致气体体积减小。
了解了气体摩尔体积公式和它的变化原理之后,我们就可以来看看它的实际应用了。在实际生活中,气体摩尔体积公式有着广泛的应用。比如,在化工生产中,我们需要计算反应物的用量和产物的生成量,这时就需要用到气体摩尔体积公式来进行计算。在医学领域,呼吸机的设计和使用也需要考虑到气体的体积和压强等参数,这些都可以通过气体摩尔体积公式来进行计算和分析。
此外,气体摩尔体积公式还可以帮助我们理解一些有趣的化学现象。比如,为什么气球在升高时会膨胀?这是因为随着海拔的升高,大气压会逐渐降低,而气球内部的气体的压强和温度基本保持不变。因此,根据气体摩尔体积公式,当压强降低时,气体摩尔体积会增大,从而导致气球膨胀。
总之,气体摩尔体积公式是化学中一个非常重要的概念,它可以帮助我们理解气体的性质和行为,并进行相关的计算和分析。通过了解气体摩尔体积的定义、公式、变化原理以及实际应用,我们可以更好地掌握这个概念,并在实际生活中加以运用。
当然,在学习和理解气体摩尔体积公式的过程中,我们也需要注意一些细节和注意事项。比如,在计算过程中要注意单位的换算和统一;在理解气体摩尔体积的变化原理时,要注意区分不同条件下气体摩尔体积的变化规律;在实际应用中,要根据具体情况选择合适的公式和方法进行计算和分析。只有这样,我们才能更好地掌握和运用气体摩尔体积公式这个有力的工具。
最后,希望这篇文章能够帮助你更好地了解和理解气体摩尔体积公式以及它的各个方面。如果你对这个话题还有任何疑问或想要深入了解更多
- 上一篇: 揭秘!王默的真实姓名究竟为何?
- 下一篇: 轻松掌握:如何用身份证号查询四级考试成绩
-
 棱锥体积公式详解,轻松掌握!资讯攻略10-30
棱锥体积公式详解,轻松掌握!资讯攻略10-30 -
 揭秘梯形体积计算的神秘公式!资讯攻略11-10
揭秘梯形体积计算的神秘公式!资讯攻略11-10 -
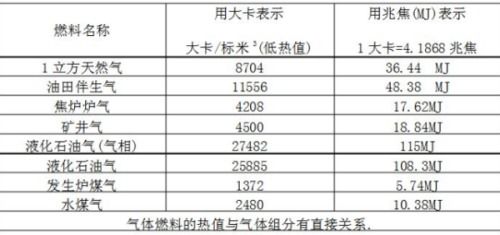 热值的计算公式是什么资讯攻略10-26
热值的计算公式是什么资讯攻略10-26 -
 揭秘梯形体积计算:轻松掌握公式秘籍资讯攻略10-30
揭秘梯形体积计算:轻松掌握公式秘籍资讯攻略10-30 -
 一键获取CBM计算公式资讯攻略10-30
一键获取CBM计算公式资讯攻略10-30 -
 揭秘SVI:深入了解这一神秘概念资讯攻略11-17
揭秘SVI:深入了解这一神秘概念资讯攻略11-17












