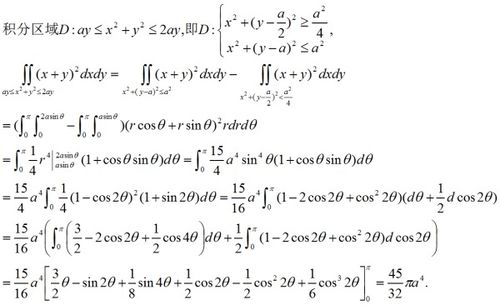掌握第一类曲线积分的高效计算方法
第一类曲线积分的基本计算方法

在微积分学中,曲线积分是一种重要的工具,用于描述沿曲线的某种物理量的累积效果。其中,第一类曲线积分(也称为对弧长的曲线积分)是最基础且常见的一种类型。这类积分的形式主要用来计算曲线上的某种密度或权重沿整个曲线的累积和,比如计算一根不均匀分布的细线的质量等。本文将详细介绍第一类曲线积分的基本概念和计算方法,并通过实例帮助读者更好地理解和掌握这一知识点。

一、第一类曲线积分的定义
设曲线L由参数方程

r(t) = (x(t), y(t), z(t)), t ∈ [α, β]
给出,f(x, y, z)是定义在曲线L上的函数。那么,函数f(x, y, z)在曲线L上的第一类曲线积分定义为
∫_L f(x, y, z) ds = ∫_α^β f(x(t), y(t), z(t)) |r'(t)| dt
其中,r'(t)是曲线L在参数t处的切向量,|r'(t)|是切向量的模,也称为曲线L在参数t处的弧微分ds。
当曲线L位于二维平面上时,可以设曲线L的参数方程为
r(t) = (x(t), y(t)), t ∈ [α, β]
此时,函数f(x, y)在曲线L上的第一类曲线积分定义为
∫_L f(x, y) ds = ∫_α^β f(x(t), y(t)) √((x'(t))^2 + (y'(t))^2) dt
二、计算步骤
计算第一类曲线积分的基本步骤如下:
1. 确定曲线的参数方程:首先,需要明确曲线的参数方程,即将曲线表示为参数t的函数。
2. 计算弧微分ds:根据曲线的参数方程,计算弧微分ds。对于三维曲线,弧微分ds = |r'(t)| dt;对于二维曲线,弧微分ds = √((x'(t))^2 + (y'(t))^2) dt。
3. 将被积函数f(x, y, z)或f(x, y)表示为参数t的函数:根据曲线的参数方程,将被积函数f(x, y, z)或f(x, y)用参数t表示出来。
4. 进行定积分计算:将上述步骤中的结果代入第一类曲线积分的定义式,得到一个关于参数t的定积分,然后利用定积分的计算方法求解该定积分。
三、实例分析
例1:计算二维曲线上的第一类曲线积分
设曲线L的方程为y = x^2,x ∈ [0, 1],求∫_L (x + y) ds。
解:
1. 确定曲线的参数方程:曲线L的方程可以写为参数方程形式r(t) = (t, t^2),t ∈ [0, 1]。
2. 计算弧微分ds:对于二维曲线,弧微分ds = √((x'(t))^2 + (y'(t))^2) dt = √(1^2 + (2t)^2) dt = √(1 + 4t^2) dt。
3. 将被积函数f(x, y)表示为参数t的函数:被积函数f(x, y) = x + y = t + t^2。
4. 进行定积分计算:将上述结果代入第一类曲线积分的定义式,得到
∫_L (x + y) ds = ∫_0^1 (t + t^2) √(1 + 4t^2) dt
这是一个关于t的定积分,可以通过换元法或分部积分法求解。经过计算,得到该定积分的值为(√5/10)(3 + 2√5)。
例2:计算三维曲线上的第一类曲线积分
设曲线L的参数方程为
r(t) = (cost, sint, t), t ∈ [0, π]
求∫_L (x^2 + y^2 + z) ds。
解:
1. 确定曲线的参数方程:曲线L的参数方程已给出为r(t) = (cost, sint, t),t ∈ [0, π]。
2. 计算弧微分ds:对于三维曲线,弧微分ds = |r'(t)| dt =
- 上一篇: 微信朋友圈秘诀:轻松发布超30秒至2分钟长视频技巧大公开!
- 下一篇: 如何轻松撰写论文大纲
-
 曲线积分的计算方法资讯攻略10-31
曲线积分的计算方法资讯攻略10-31 -
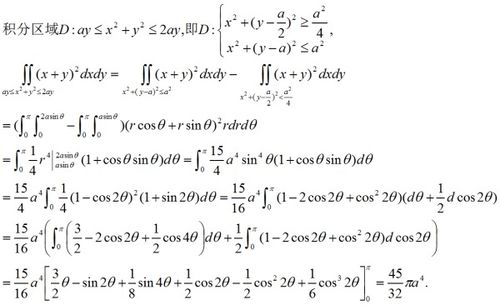 掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24
掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24 -
 PPT中如何制作曲线图?资讯攻略10-30
PPT中如何制作曲线图?资讯攻略10-30 -
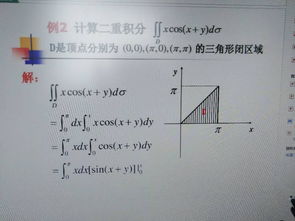 二重积分计算方法揭秘,附上一个简单易懂例题解析资讯攻略12-06
二重积分计算方法揭秘,附上一个简单易懂例题解析资讯攻略12-06 -
 双曲线的顶点坐标公式及求解方法资讯攻略10-28
双曲线的顶点坐标公式及求解方法资讯攻略10-28 -
 拉格朗日定理的具体公式是什么资讯攻略11-07
拉格朗日定理的具体公式是什么资讯攻略11-07