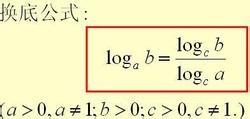揭秘:log函数的定义域究竟隐藏着什么奥秘?
在数学的世界里,对数函数(log函数)以其独特的性质和广泛的应用而著称。对于许多初学者而言,理解对数函数的定义域是掌握这一概念的关键一步。那么,log函数的定义域究竟是什么呢?本文将带你深入探讨,揭开对数函数定义域的神秘面纱。

首先,我们要明确对数函数的基本形式。对数函数通常以y=logₐx(其中a为底数,x为真数)的形式出现。这里的底数a是一个正数,且a≠1。对数函数表达的是,以a为底的对数等于某个数y,当且仅当a的y次方等于x。换句话说,对数函数是指数函数的反函数。

接下来,我们重点讨论对数函数的定义域。定义域是函数自变量的取值范围,对于对数函数而言,真数x的取值范围就是其定义域。那么,x的取值需要满足哪些条件呢?
首先,由于对数函数是基于指数函数定义的,而指数函数的底数和指数都是实数,因此真数x也必须是实数。这是对数函数定义域的一个基本要求。
其次,由于指数函数的值域是正实数集(不包括0),因此对数函数的真数x必须大于0。这是因为在实数范围内,任何正数的任何次幂都是正数,而0的任何正次幂都是0(0的0次幂在数学中是未定义的),负数的实数次幂在实数范围内没有意义(因为会得到虚数)。因此,对于对数函数y=logₐx而言,只有当x>0时,函数才有意义。
综上所述,对数函数y=logₐx的定义域是所有大于0的实数,即(0,+∞)。这是对数函数定义域的核心内容。
接下来,我们进一步探讨对数函数定义域的一些重要性质和推论。
1. 唯一性:对于给定的底数a和真数x(x>0),对数函数y=logₐx的值是唯一的。这是因为指数函数y=a^x是单调增函数(当a>1时)或单调减函数(当0
2. 连续性:对数函数在其定义域内是连续的。这意味着,如果x在(0,+∞)内连续变化,那么y=logₐx的值也将连续变化。这一性质使得对数函数在分析和计算中具有很高的应用价值。
3. 单调性:对数函数在其定义域内具有单调性。当底数a>1时,对数函数是单调增函数;当0
- 上一篇: 制作糍粑鱼的详细步骤
- 下一篇: 《《斛珠夫人》揭秘:琅嬛的最终结局究竟是什么?》
-
 揭秘:对数的定义域究竟隐藏着什么奥秘?资讯攻略11-03
揭秘:对数的定义域究竟隐藏着什么奥秘?资讯攻略11-03 -
 揭秘:log2到底是什么?一文读懂!资讯攻略11-10
揭秘:log2到底是什么?一文读懂!资讯攻略11-10 -
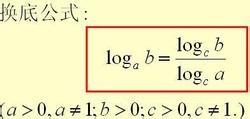 对数基本公式:详解log函数的定义与应用资讯攻略10-26
对数基本公式:详解log函数的定义与应用资讯攻略10-26 -
 三角函数cot的定义及公式是什么?资讯攻略11-24
三角函数cot的定义及公式是什么?资讯攻略11-24 -
 掌握log函数求导公式,轻松解决数学问题资讯攻略11-09
掌握log函数求导公式,轻松解决数学问题资讯攻略11-09 -
 探索对数函数导数的奥秘资讯攻略11-04
探索对数函数导数的奥秘资讯攻略11-04