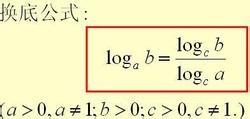探索对数函数导数的奥秘
2024-11-04 08:40:11
对数函数的导数探索

在数学中,对数函数与导数都是极为重要且应用广泛的概念。对数函数,以其独特的性质和形式,在解决多种实际问题时发挥着不可替代的作用;而导数,则作为微积分的基础,是研究函数变化率的重要工具。当这两者相遇——即求对数函数的导数时,我们会发现一个既深刻又美丽的数学结论。

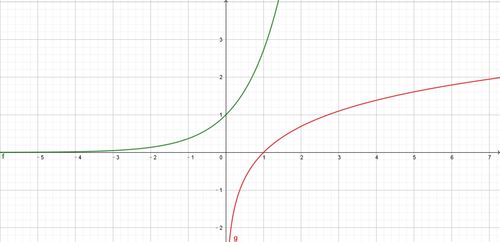
首先,我们来回顾一下对数函数的基本概念。对数函数通常表示为y=logₐx(其中a为底数,x为真数),它表示以a为底x的对数。对数函数具有一些基本的性质,如当底数a大于1时,函数是增函数;当0
现在,我们回到主题——对数函数的导数。为了求出对数函数y=logₐx的导数,我们可以利用导数的定义和链式法则进行推导。
因此,我们得出lim(Δx→0){ln[(1+Δx/x)]/(Δx/x)}=1。将这个结果代入原极限中,我们得到f'(x)=1/x。所以,对于函数y=lnx,其导数为y'=1/x。
因此,我们得出了对数函数y=logₐx的导数公式:y'=1/(xlna)。这个公式表明,对于任意以a为底的对数函数,其导数都与x成反比,并且与底数a的自然对数lna有关。
- 上一篇: IMEI码是什么?如何快速查询?
- 下一篇: 蛇结编织教程:详细图解步骤
相关下载
相关攻略
-
 掌握log函数求导公式,轻松解决数学问题资讯攻略11-09
掌握log函数求导公式,轻松解决数学问题资讯攻略11-09 -
 揭秘:log函数的定义域究竟隐藏着什么奥秘?资讯攻略11-23
揭秘:log函数的定义域究竟隐藏着什么奥秘?资讯攻略11-23 -
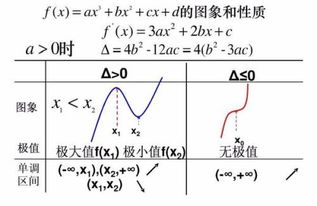 揭秘三次函数的图像奥秘与独特性质资讯攻略11-04
揭秘三次函数的图像奥秘与独特性质资讯攻略11-04 -
 探索数学奥秘:ln1、ln(-1)、Ln1、Ln(-1)的神奇值是多少?资讯攻略11-05
探索数学奥秘:ln1、ln(-1)、Ln1、Ln(-1)的神奇值是多少?资讯攻略11-05 -
 cot导数的定义与计算方法资讯攻略11-24
cot导数的定义与计算方法资讯攻略11-24 -
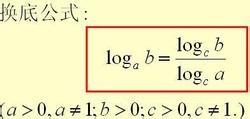 对数基本公式:详解log函数的定义与应用资讯攻略10-26
对数基本公式:详解log函数的定义与应用资讯攻略10-26