揭秘双曲线的奇妙知识点:探索无限延伸的几何之美
双曲线,这一数学概念,在几何学、代数学乃至物理学等多个领域中扮演着重要角色。它不仅是高中数学课程中的一部分,更是深入理解更高级数学知识的基础。对于那些对双曲线充满好奇、想要深入探索其奥秘的朋友,以下是一篇简明扼要又充满趣味的双曲线知识点介绍。
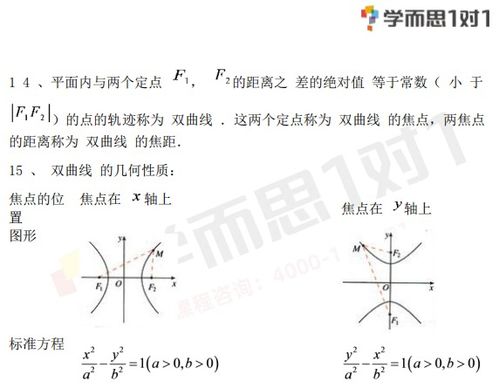
首先,让我们从双曲线的定义开始。双曲线,顾名思义,是由两条看似无穷远又彼此分离的曲线组成的图形。更严谨地说,双曲线是平面内与两个定点(焦点)的距离之差的绝对值等于定长(实轴长)的点的轨迹。这两个定点就是双曲线的焦点,而定长则是双曲线的实轴长。值得注意的是,这里的“距离之差”必须取绝对值,这保证了轨迹的连续性和对称性。

双曲线的标准方程有多种形式,根据焦点的位置和坐标系的设定,最常见的是以下两种:
1. 焦点在x轴上的双曲线方程:x^2/a^2 - y^2/b^2 = 1(a > 0, b > 0)。在这个方程中,a代表实轴长的一半,b代表虚轴长的一半(虚轴是与实轴垂直、经过原点、且双曲线渐近线所在的直线),c则代表焦点到原点的距离,它们之间满足关系c^2 = a^2 + b^2。
2. 焦点在y轴上的双曲线方程:y^2/a^2 - x^2/b^2 = 1(a > 0, b > 0)。这种情况下,双曲线的形状与焦点在x轴上的双曲线相似,只是方向发生了旋转。
双曲线的几何性质丰富多样,以下是一些重要的知识点:
对称性:双曲线关于x轴和y轴都是对称的。这意味着,如果点(x, y)在双曲线上,那么点(-x, y)、(x, -y)和(-x, -y)也都在双曲线上。
渐近线:双曲线有两条渐近线,它们是两条直线,双曲线会随着x或y的增大而越来越接近这两条直线,但永远不会相交。对于焦点在x轴上的双曲线,其渐近线方程为y = ±(b/a)x;对于焦点在y轴上的双曲线,其渐近线方程为x = ±(b/a)y。
离心率:双曲线的离心率e是一个重要的参数,它反映了双曲线的“扁平”程度。离心率e的定义为e = c/a,其中c是焦点到原点的距离,a是实轴长的一半。离心率越大,双曲线越“扁平”;离心率越小,双曲线越接近一个圆(当e=1时,双曲线退化为两条直线,即渐近线)。
焦点与顶点:双曲线的焦点是两个特定的点,它们位于双曲线的两侧,是使双曲线上任意一点到两焦点的距离之差等于定长的点。而顶点则是双曲线与实轴的交点,它们位于双曲线的中心位置,是离原点最近的点。
面积与周长:与圆或椭圆不同,双曲线的面积和周长没有简单的公式来计算。然而,可以通过积分等数学方法近似求解双曲线围成的面积或双曲线某一部分的弧长。
双曲线不仅在几何学中有重要地位,它在物理学和工程学中也有着广泛的应用。例如,在光学中,双曲线形状的反射面可以使光线汇聚于一点(类似于抛物面镜),这在天文望远镜和激光器中有着重要应用。在工程学中,双曲线形状的桥梁或拱门设计可以在保证结构强度的同时减轻重量,提高材料的利用效率。
此外,双曲线还与数学中的其他概念紧密相连。例如,在复分析中,双曲线可以看作是某种类型的黎曼面;在微分几何中,双曲线可以看作是双曲空间中的直线;在射影几何中,双曲线则可以通过投影变换与其他类型的二次曲线相互转换。
对于想要深入学习双曲线的朋友来说,掌握上述知识点只是第一步。接下来,你可以尝试解决一些与双曲线相关的数学问题,如求解双曲线上某一点的坐标、计算双曲线的面积或周长(近似值)、分析双曲线在不同参数下的形状变化等。这些问题不仅有助于巩固你对双曲线知识的理解,还能培养你的数学思维和解决问题的能力。
此外,你还可以通过阅读相关数学书籍或在线资源来进一步拓宽视野。例如,《几何原本》、《解析几何》等经典著作中都有关于双曲线的详细讨论;而互联网上的数学论坛、在线课程和教育平台则提供了更多互动式学习和交流的机会。
总之,双曲线是一个既神秘又迷人的数学概念。它不仅在几何学中占据重要地位,还与物理学、工程学以及数学中的其他分支紧密相连。通过深入学习双曲线的知识点并尝试解决相关问题,你将能够领略到数学世界的无穷魅力和无限可能。希望这篇介绍能够激发你对双曲线的好奇心并引导你踏上探索数学奥秘的旅程!
- 上一篇: 揭秘“七十三八十四”背后的神秘说法
- 下一篇: 元歌的17种连招口诀分别是什么?
-
 双曲线的顶点坐标公式及求解方法资讯攻略10-28
双曲线的顶点坐标公式及求解方法资讯攻略10-28 -
 轻松学会!萌趣蝙蝠简笔画教程资讯攻略10-25
轻松学会!萌趣蝙蝠简笔画教程资讯攻略10-25 -
 揭秘:圆形面积计算的神奇公式是什么?资讯攻略10-31
揭秘:圆形面积计算的神奇公式是什么?资讯攻略10-31 -
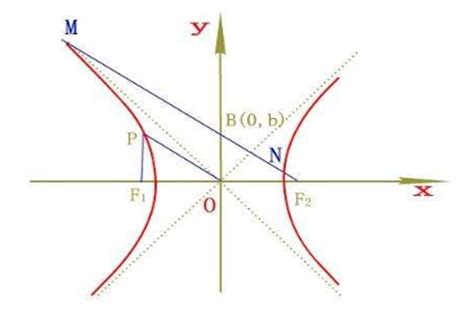 双曲线离心率公式具体有哪些?资讯攻略11-04
双曲线离心率公式具体有哪些?资讯攻略11-04 -
 如何绘制莱洛三角形?资讯攻略11-30
如何绘制莱洛三角形?资讯攻略11-30 -
 揭秘圆周率:探寻隐藏的数学奥秘与规律资讯攻略11-19
揭秘圆周率:探寻隐藏的数学奥秘与规律资讯攻略11-19












