双曲线离心率公式具体有哪些?
双曲线作为圆锥曲线的重要类型之一,在解析几何和代数运算中占据着重要的地位。而双曲线的离心率作为描述其形状的关键参数,更是学习和研究双曲线时不可或缺的知识点。本文将详细介绍双曲线离心率的公式及相关内容,旨在帮助读者深入理解这一重要概念。
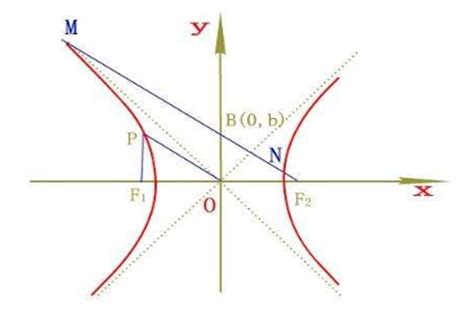
首先,我们需要明确双曲线的基本定义。在平面内,双曲线可以定义为与两个固定点(焦点)的距离之差为常数的点的轨迹。另外,双曲线还可以看作是平面交截直角圆锥面的两半。这些定义为我们后续理解双曲线的性质提供了基础。
离心率,作为描述双曲线形状的一个重要参数,具有多种表达形式。首先,最基本的双曲线离心率公式是e=c/a,其中c是双曲线焦点到中心的距离,a是双曲线半轴的长度。这一公式直接反映了离心率与焦点和半轴长度之间的关系。
在双曲线的标准方程x^2/a^2 - y^2/b^2 = 1中,b^2=a^2+c^2。因此,我们可以将离心率公式进一步表示为e=c/a=√(b^2-a^2)/a。这个公式揭示了离心率与双曲线方程参数之间的直接联系,使得我们能够通过方程参数来求解离心率。
值得注意的是,虽然b^2=a^2+c^2这一关系在形式上与椭圆的焦点距离公式相似,但双曲线的离心率e的取值范围是e∈(1,+∞),这与椭圆的离心率e∈(0,1)有着本质的区别。这一区别反映了双曲线和椭圆在上的形状显著差异。
此外,离心率还可以通过双曲线的渐近线与正半轴的夹角θ来表示。由于c/a=cos(θ),我们可以将离心率公式进一步转化为e=√(cos^2(θ)+1)。这一公式揭示了离心率与双曲线渐近线斜率之间的关系,为我们提供了一种新的理解和计算离心率的方法。
离心率在双曲线中扮演着至关重要的角色。它不仅是描述双曲线形状的重要参数,还直接影响了双曲线的许多其他性质。例如,在双曲线中,当离心率越大时,其形状从扁狭逐渐变得越开阔,即双曲线的“张口”逐渐增大。这一性质使得我们能够通过观察离心率的大小来直观地判断双曲线的形状特征。
在数学和物理学中,离心率的概念有着广泛的应用。在圆锥曲线的相关问题中,离心率经常以参变量的形式出现。根据问题给出的条件,我们可以建立离心率e的不等式,通过解不等式来解决问题,并确定离心率的取值范围。这种方法在解析几何和代数运算中具有重要的实用价值。
在物理学中,离心率的概念最早是为描述太阳系中行星运行轨道的形状而引入的。它表示某一椭圆轨道与理想圆环的偏离程度,又称偏心率。虽然这里讨论的是椭圆轨道的离心率,但双曲线的离心率概念同样具有类似的物理意义。它描述了双曲线轨道与理想直线轨道的偏离程度,为我们提供了一种描述和分析复杂轨道形状的有效工具。
除了基本的离心率公式外,我们还可以通过一些特殊的方法来计算双曲线的离心率。例如,利用双曲线的焦点三角形来求解离心率。双曲线的焦点三角形指的是双曲线上任意一点P与双曲线左、右两个焦点F1、F2所构成的三角形。通过求解这个三角形的边长和角度关系,我们可以推导出离心率的表达式。
另外,我们还可以利用双曲线的焦点弦来求解离心率。连接双曲线上任意的两点A、B得到的线段AB叫做双曲线的弦。如果这条弦AB经过双曲线的焦点F,那么称这条弦AB为双曲线的焦点弦。通过求解焦点弦的长度和位置关系,我们同样可以推导出离心率的表达式。
这些方法不仅丰富了求解离心率的手段,还为我们提供了一种直观理解和分析双曲线性质的有效途径。通过运用这些方法,我们可以更加深入地理解双曲线的形状特征和变化规律。
在实际应用中,双曲线的离心率公式具有广泛的用途。例如,在工程设计、物理模拟和计算机科学等领域中,我们经常需要利用双曲线的性质来描述和分析复杂系统的行为。这时,离心率作为一个重要的参数,可以帮助我们更准确地把握系统的动态特征和变化趋势。
此外,在高考等考试中,双曲线的离心率也是一个重要的考点。通过理解和掌握离心率公式及其相关性质,我们可以更加有效地解决相关的数学问题,提高考试成绩。
综上所述,双曲线的离心率公式是描述其形状的重要参数之一。通过理解和掌握这些公式及其相关性质,我们可以更加深入地理解双曲线的形状特征和变化规律。同时,这些公式也为我们在实际应用中提供了有效的工具和方法来分析和解决问题。因此,在学习和研究双曲线时,我们应该充分重视离心率的概念和应用,努力掌握相关的知识和技能。
- 上一篇: 三星手机客服,一键速联指南!
- 下一篇: 2021恐怖童谣揭秘:红伞伞背后的诡异暗示
-
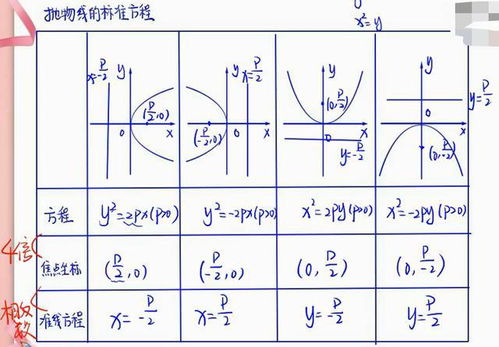 如何绘制双曲线的准线资讯攻略11-01
如何绘制双曲线的准线资讯攻略11-01 -
 拉格朗日定理的具体公式是什么资讯攻略11-07
拉格朗日定理的具体公式是什么资讯攻略11-07 -
 双曲线的顶点坐标公式及求解方法资讯攻略10-28
双曲线的顶点坐标公式及求解方法资讯攻略10-28 -
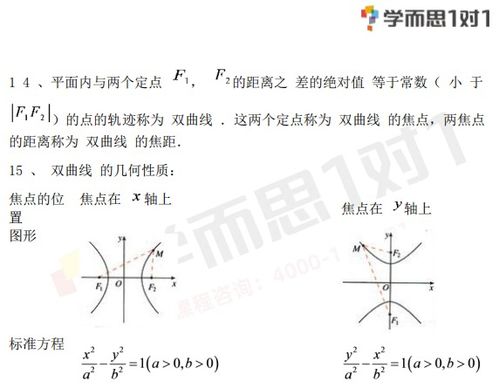 揭秘双曲线的奇妙知识点:探索无限延伸的几何之美资讯攻略11-15
揭秘双曲线的奇妙知识点:探索无限延伸的几何之美资讯攻略11-15 -
 曲线积分的计算方法资讯攻略10-31
曲线积分的计算方法资讯攻略10-31 -
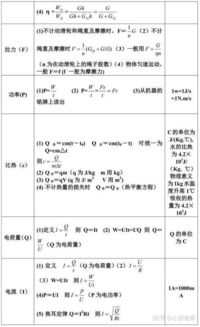 资料分析常用公式有哪些汇总?资讯攻略11-02
资料分析常用公式有哪些汇总?资讯攻略11-02












