抛物线相关的所有公式总结有哪些?
抛物线,作为数学中一个重要的几何图形,在平面内与一个定点F和一条定直线的距离相等的点的轨迹构成。定点F被称为抛物线的焦点,而定直线则被称为抛物线的准线。为了更好地理解和应用抛物线,我们总结了一些关键的公式和概念,旨在以通俗易懂的方式介绍这些知识点。

抛物线的一般式
抛物线的一般式方程为:

y = ax² + bx + c

其中,a、b、c为常数,且a ≠ 0。这个方程是抛物线最基本的表达形式,通过它可以描述各种形态的抛物线。
当a > 0时,抛物线开口向上;
当a < 0时,抛物线开口向下;
当c = 0时,抛物线经过原点;
当b = 0时,抛物线的对称轴为y轴。
抛物线的顶点式
抛物线的顶点式方程为:
y = a(x - h)² + k
其中,a、h、k为常数,且a ≠ 0。顶点式方程通过h和k直接给出了抛物线的顶点坐标(h, k)。这个方程形式非常适合用来求解抛物线的最大值或最小值,因为顶点的y坐标就是函数的极值。
顶点坐标:(h, k)
当a > 0时,顶点为最小值点;
当a < 0时,顶点为最大值点。
抛物线的交点式(两根式)
抛物线的交点式方程为:
y = a(x - x₁)(x - x₂)
其中,a ≠ 0,x₁和x₂是抛物线与x轴两交点的横坐标。交点式方程揭示了抛物线与x轴交点的位置,当且仅当抛物线与x轴有两个交点时,此方程成立。
交点坐标:(x₁, 0) 和 (x₂, 0)
交点式方程实际上是由一般式方程通过因式分解得到的,因此x₁和x₂也是方程ax² + bx + c = 0的两个实数根。
抛物线的标准方程
根据抛物线的开口方向和位置,其标准方程有以下几种形式:
1. y² = 2px(焦点在x轴正半轴上)
焦点坐标:(p/2, 0)
准线方程:x = -p/2
2. y² = -2px(焦点在x轴负半轴上)
焦点坐标:(-p/2, 0)
准线方程:x = p/2
3. x² = 2py(焦点在y轴正半轴上)
焦点坐标:(0, p/2)
准线方程:y = -p/2
4. x² = -2py(焦点在y轴负半轴上)
焦点坐标:(0, -p/2)
准线方程:y = p/2
抛物线的其他重要概念和公式
抛物线的对称轴
对于一般式方程y = ax² + bx + c,抛物线的对称轴为直线x = -b/(2a)。
抛物线的焦距和准距
焦距(即焦点到准线的距离)为p,准距(即准线到原点的距离)也为p/2(当焦点在x轴上时)或p(当焦点在y轴上时,需乘以相应的系数)。
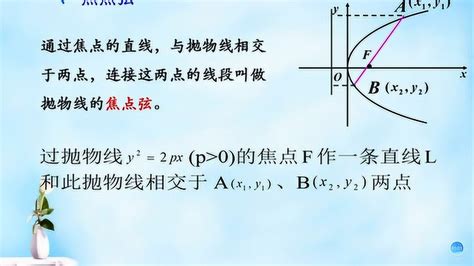
抛物线的焦点弦公式
当抛物线焦点在x轴上时,焦点弦只和两焦点的横坐标有关;当抛物线焦点在y轴上时,焦点弦只和两焦点的纵坐标有关。具体的焦点弦公式可能涉及复杂的几何关系和代数运算,通常在实际问题中需要根据具体情况进行推导。
抛物线的通径
通径是过焦点且垂直于对称轴的相交弦。对于标准方程y² = 2px,通径的长度为2p;对于标准方程x² = 2py,通径的长度也为2p(但方向不同)。
抛物线的法线
过抛物线上一点可以作一条切线,过切点所作垂直于切线的直线叫做抛物线在这点的法线。抛物线的法线有一条重要性质:经过抛物线上一点作一直线平行于抛物线的轴(即对称轴),那么经过这一点的法线平分这条直线和这点与焦点连线的夹角。
应用实例
1. 求解抛物
- 上一篇: 经典油焖茄子制作教程
- 下一篇: 掌握顶尖销售策略:解锁销售高手的必备技巧
-
 揭秘!抛物线焦点弦的神奇长度公式,让你秒变几何达人资讯攻略10-27
揭秘!抛物线焦点弦的神奇长度公式,让你秒变几何达人资讯攻略10-27 -
 顶点公式的具体表达是什么?资讯攻略12-03
顶点公式的具体表达是什么?资讯攻略12-03 -
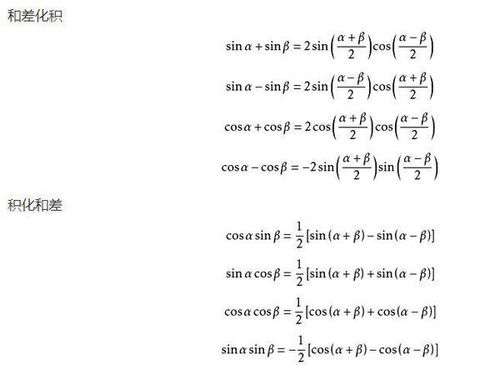 掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19
掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19 -
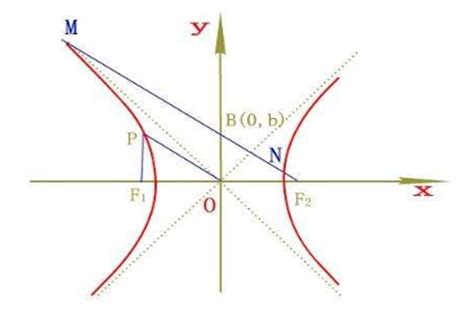 双曲线离心率公式具体有哪些?资讯攻略11-04
双曲线离心率公式具体有哪些?资讯攻略11-04 -
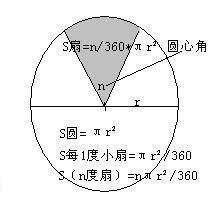 扇形的所有重要公式汇总资讯攻略10-28
扇形的所有重要公式汇总资讯攻略10-28 -
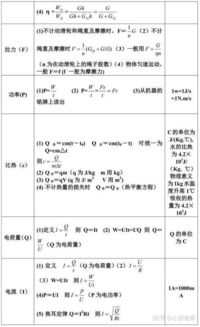 资料分析常用公式有哪些汇总?资讯攻略11-02
资料分析常用公式有哪些汇总?资讯攻略11-02