四棱柱侧面展开图的形状揭秘
四棱柱,作为一种基础的三维几何体,在几何学、建筑学、工程学等多个领域都扮演着重要角色。当我们提及四棱柱的侧面展开图时,实际上是将其三维形态通过二维平面的方式展现出来,这一过程不仅有助于我们更直观地理解四棱柱的结构特征,还能激发对几何形态、空间变换以及应用实践等多方面的思考。

形态解析:从三维到二维的映射
四棱柱,顾名思义,是一个顶面与底面均为四边形且平行,侧面为矩形的立体图形。其侧面展开图,则是将四棱柱的每一个侧面沿着它们的边缘展开至同一平面内,形成的一个组合图形。根据四棱柱底面四边形的不同(如正方形、矩形、平行四边形等),侧面展开图也会呈现出多样化的形态。
正方形底面:若四棱柱底面为正方形,其侧面展开图将是由四个完全相同的正方形拼接而成的大正方形,每个小正方形代表一个侧面,它们共享一条边以模拟原四棱柱的连续性。
矩形底面:当底面为矩形时,侧面展开图则为四个形状相同但大小可能不一的矩形组成,这些矩形的长边相连,形成一条直线,短边则各自独立,体现了底面长宽比例对侧面形状的影响。
平行四边形底面:对于底面为平行四边形的四棱柱,其侧面展开图则更为复杂,但仍保持由四个矩形组成的基本结构,只不过这些矩形的长边或短边可能不再平行,反映出底面斜边导致的侧面倾斜。
空间变换:理解维度的跨越
侧面展开图不仅是一个静态的图形展示,更是一次从三维到二维空间变换的生动演绎。这一过程中,我们需要理解“展开”这一动作所蕴含的数学原理,即如何通过保留长度、角度等度量属性,在二维平面上准确反映三维空间的结构。
面积守恒:在展开过程中,四棱柱各个侧面的面积之和等于展开图的面积,这一原则确保了空间与平面之间量的守恒。通过观察展开图,我们可以轻松计算出四棱柱的侧面积,无需回到三维空间中进行复杂的测量。
展开路径:不同的展开路径会得到不同的展开图,但所有合法的展开图在拓扑上都是等价的,即它们可以通过剪裁、拼接等操作相互转换。这一特性强调了空间几何的灵活性,同时也为我们在实际应用中提供了多样化的解决方案。
几何直觉:通过侧面展开图,我们可以直观地感受到三维空间中直线、平面之间的相对位置关系,这对于培养空间想象力、解决立体几何问题至关重要。
应用实践:从理论到生活的桥梁
四棱柱侧面展开图的理论价值,在诸多实践领域得到了广泛应用,无论是建筑设计、包装设计,还是计算机图形学、动画制作,都能见到其身影。
建筑设计:在建筑设计中,利用四棱柱侧面展开图可以快速绘制建筑表皮的展开样式,便于计算材料用量、设计图案布局,尤其是在需要精确控制材料切割和拼接的场合,如建筑幕墙、屋顶结构等。
包装设计:包装设计师常需将三维产品转化为二维图纸以进行打印和制造。对于盒装产品,其包装盒往往可以视为一个特殊的四棱柱,侧面展开图能够帮助设计师精确计算包装材料的尺寸,优化折叠结构,确保产品既能安全包装又能节约材料。
计算机图形学:在计算机图形学中,四棱柱侧面展开图是进行纹理映射、三维渲染等操作的基础。通过将三维模型拆解为平面片(如侧面展开图),可以更容易地在二维平面上进行纹理设计,再通过算法将纹理贴回三维模型,实现逼真的视觉效果。
动画制作:在动画制作领域,特别是三维动画中,角色和场景的建模往往涉及到复杂的几何体变换。四棱柱侧面展开图作为理解和实现几何体折叠、展开动画的重要工具,有助于动画师准确捕捉和表现物体的形态变化,增强动画的真实感和动态效果。
教育意义:培养空间思维与创新能力
在基础教育和高等教育中,四棱柱侧面展开图也是几何学教学的重要内容之一。它不仅能够帮助学生掌握基本的几何概念和操作方法,更重要的是,通过动手绘制、分析展开图,学生可以在实践中逐步建立起空间观念,提高空间思维能力。
动手实践:通过亲自动手绘制四棱柱及其侧面展开图,学生可以从操作中直观地感受到三维到二维的转换过程,加深对几何体结构特征的理解。
问题解决:解决与侧面展开图相关的问题,如最小化材料用量、设计特定图案的包装等,能够锻炼学生的创新思维和问题解决能力。
跨学科应用:引导学生思考四棱柱侧面展开图在其他学科或领域的应用,如物理中的受力分析、经济学中的成本优化等,可以拓宽学生的视野,促进跨学科学习。
综上所述,四棱柱侧面展开图不仅是连接
- 上一篇: 轻松学会红糖鸡蛋的美味做法!
- 下一篇: 警务辅助人员看护岗位职责解析
-
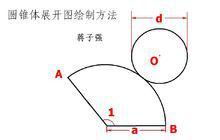 如何绘制圆锥体的展开图资讯攻略11-05
如何绘制圆锥体的展开图资讯攻略11-05 -
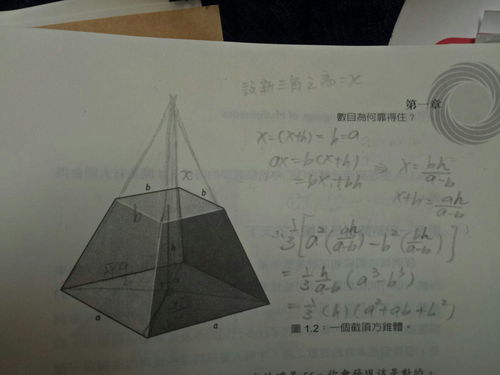 棱锥体积公式详解,轻松掌握!资讯攻略10-30
棱锥体积公式详解,轻松掌握!资讯攻略10-30 -
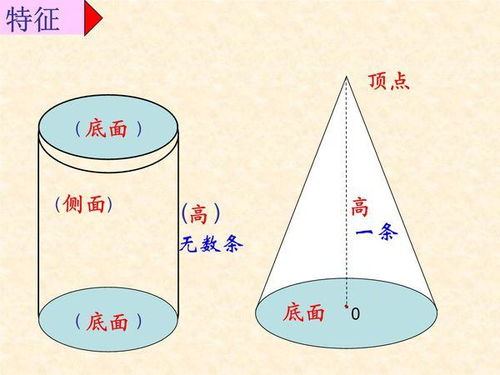 圆柱与圆锥的关联解析资讯攻略11-03
圆柱与圆锥的关联解析资讯攻略11-03 -
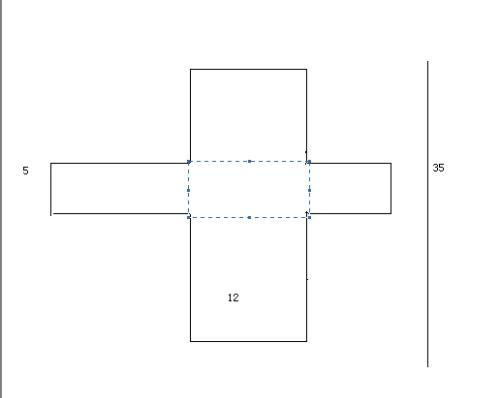 长方体展开图有几种常见的形式?资讯攻略11-12
长方体展开图有几种常见的形式?资讯攻略11-12 -
 CAD中轻松绘制圆锥展开图的方法资讯攻略11-05
CAD中轻松绘制圆锥展开图的方法资讯攻略11-05 -
 揭秘!棱锥的多种分类,你了解几种?资讯攻略10-25
揭秘!棱锥的多种分类,你了解几种?资讯攻略10-25












